Question

【题目】已知直线的参数方程为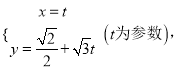若以直角坐标系xOy的O点为极点，Ox方向为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程为

(1)求直线的斜率和曲线C的直角坐标方程；

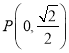(2)若直线与曲线C交于A、B 两点，设点，求|PA|+|PB|.

Answer 1

【答案】(1) 直线的斜率为, 曲线C的直角坐标方程为（x﹣）2+（y﹣）2=1

;(2) |PA|+|PB|=.

【解析】试题分析：（1）直线l的参数方程为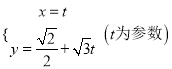 ，消去参数t化为普通方程可得，进而得到倾斜角．由曲线C的极坐标方程得到：ρ2=2ρcos（θ﹣），利用ρ2=x2+y2，即可化为直角坐标方程．

（2）将|PA|+|PB|转化为求|AB|来解答．

试题解析：

（1）直线的斜率为，直线l倾斜角为

由曲线C的极坐标方程得到：ρ2=2ρcos（θ﹣），利用ρ2=x2+y2，得到曲线C的直角坐标方程为（x﹣）2+（y﹣）2=1

（2）点P（0， ）在直线l上且在圆C内部，所以|PA|+|PB|=|AB|

直线l的直角坐标方程为y=x+

所以圆心（， ）到直线l的距离d=．所以|AB|=，即|PA|+|PB|=