题目内容
已知函数f(x)＝|lgx|.若0<a<b，且f(a)＝f(b)，则a＋2b的取值范围是( )．
A．(2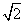
，＋∞) B．[2，＋∞)
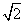C．(3，＋∞) D．[3，＋∞)
C
解析 由已知条件0<a<1<b和f(a)＝f(b)得，－lg a＝lg b，则lg a＋lg b＝0，ab＝1，因此a＋2b＝a＋
，由对勾函数知y＝x＋
在(0,1)单调递减，得a＋2b>3，即a＋2b的取值范围是(3，＋∞)．
练习册系列答案
相关题目
)
