题目内容
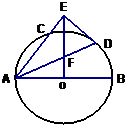（2011•西山区模拟）如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于D，DE⊥AC交AC延长线于点E，OE交AD于点F．（Ⅰ）求证：DE是⊙O的切线；
（Ⅱ）若
| AC |
| AB |
| 3 |
| 5 |
| AF |
| DF |
分析：（Ⅰ）根据OA=OD，得到∠ODA=∠OAD，结合AD是∠BAC的平分线，得到∠OAD=∠DAC=∠ODA，可得OD∥AE．再根据DE⊥AE，得到DE⊥OD，结合圆的切线的判定定理，得到DE是⊙O的切线．
（II）连接BC、DB，过D作DH⊥AB于H，因为AB是⊙O的直径，所以在Rt△ACB中，求出cos∠CAB=
=
，再利用OD∥AE，所以∠DOH=∠CAB，得到Rt△HOD中，cos∠DOH=
=cos∠CAB=
．设OD=5x，则AB=10x，OH=3x，用勾股定理，在Rt△HOD中算出DH=4x，再在Rt△HAD中，算出AD2=80x2．最后利用△ADE∽△ADB，得到AD2=AE•AB=AE•10x，从而AE=8x，再结合△AEF∽△ODF，得出
=
=
．
（II）连接BC、DB，过D作DH⊥AB于H，因为AB是⊙O的直径，所以在Rt△ACB中，求出cos∠CAB=
| AC |
| AB |
| 3 |
| 5 |
| OH |
| OD |
| 3 |
| 5 |
| AF |
| DF |
| AE |
| DO |
| 8 |
| 5 |
解答：证明：（Ⅰ）连接OD，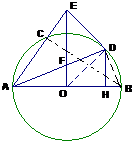
∵OA=OD，∴∠ODA=∠OAD
∵∠BAC的平分线是AD
∴∠OAD=∠DAC
∴∠DAC=∠ODA，可得OD∥AE…（3分）
又∵DE⊥AE，∴DE⊥OD
∵OD是⊙O的半径
∴DE是⊙O的切线．…（5分）
（Ⅱ）连接BC、DB，过D作DH⊥AB于H，
∵AB是⊙O的直径，
∴∠ACB=90°，
Rt△ABC中，cos∠CAB=
=
∵OD∥AE，∴∠DOH=∠CAB，
∴cos∠DOH=cos∠CAB=
．
∵Rt△HOD中，cos∠DOH=
，
∴
=
，设OD=5x，则AB=10x，OH=3x，
∴Rt△HOD中，DH=
=4x，AH=AO+OH=8x，
Rt△HAD中，AD2=AH2+DH2=80x2…（8分）
∵∠BAD=∠DAE，∠AED=∠ADB=90°
∴△ADE∽△ADB，可得
=
，
∴AD2=AE•AB=AE•10x，而AD2=80x2
∴AE=8x
又∵OD∥AE，
∴△AEF∽△ODF，可得
=
=
…（10分）
∵OA=OD，∴∠ODA=∠OAD
∵∠BAC的平分线是AD
∴∠OAD=∠DAC
∴∠DAC=∠ODA，可得OD∥AE…（3分）
又∵DE⊥AE，∴DE⊥OD
∵OD是⊙O的半径
∴DE是⊙O的切线．…（5分）
（Ⅱ）连接BC、DB，过D作DH⊥AB于H，
∵AB是⊙O的直径，
∴∠ACB=90°，
Rt△ABC中，cos∠CAB=
| AC |
| AB |
| 3 |
| 5 |
∵OD∥AE，∴∠DOH=∠CAB，
∴cos∠DOH=cos∠CAB=
| 3 |
| 5 |
∵Rt△HOD中，cos∠DOH=
| OH |
| OD |
∴
| OH |
| OD |
| 3 |
| 5 |
∴Rt△HOD中，DH=
| OD2-OH2 |
Rt△HAD中，AD2=AH2+DH2=80x2…（8分）
∵∠BAD=∠DAE，∠AED=∠ADB=90°
∴△ADE∽△ADB，可得
| AD |
| AE |
| AB |
| AD |
∴AD2=AE•AB=AE•10x，而AD2=80x2
∴AE=8x
又∵OD∥AE，
∴△AEF∽△ODF，可得
| AF |
| DF |
| AE |
| DO |
| 8 |
| 5 |
点评：本题以角平分线和圆中的垂直线段为载体，通过证明圆的切线和求线段的比，考查了相似三角形的性质、相似三角形的判定、圆的切线的判定定理等知识点，属于中档题．
练习册系列答案
相关题目