题目内容
在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题,求:(1)第1次抽到理科题的概率;
(2)第1次和第2次都抽到理科题的概率;
(3)在第1次抽到理科题的条件下,第2次抽到理科题的概率.
分析:
(1)(2)属于古典概型,(3)利用条件概率公式P(B|A)=![]() 求解.
求解.
解:设第1次抽到理科题为事件A,第2次抽到理科题为事件B,则第1次和第2次都抽到理科题为事件AB.
(1)从5道题中不放回地依次抽取2道题的事件数为n(Ω)=![]() =20.
=20.
根据分步乘法计数原理,n(A)=![]() ×A
×A![]() =12,于是
=12,于是
P(A)=![]() .
.
(2)因为n(AB)=A![]() =6,所以
=6,所以
P(AB)=![]()
(3)方法1:由(1)(2)可得,在第1次抽到理科题的条件下,第2次抽到理科题的概率为
P(B|A)=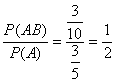 .
.
方法2:因为n(AB)=6,n(A)=12,所以P(B|A)=![]() .
.
绿色通道:利用条件概率公式求解时,求事件AB的概率(或其基本事件个数)是解决问题的关键.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
在5道题中有3道理科题和2道文科题,如果不放回地依次抽取2道题.在第一次抽到理科题的条件下,第2次抽到理科题的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|