题目内容
（2013•浙江模拟）已知同一平面上的向量
，
，
，
满足如下条件：
①|
+
|=|
|=2；
②(
+
)•
=0；
③|
+
|=|
-
|，
则|
|的最大值与最小值之差是
| PA |
| PB |
| AQ |
| BQ |
①|
| PA |
| PB |
| AB |
②(
| ||
|
|
| ||
|
|
| BQ |
③|
| AB |
| AQ |
| AB |
| AQ |
则|
| PQ |
2
2
．分析：根据②③判断出四边形ABCQ是正方形，并建立坐标系，找出A，B，C及Q的坐标，设出P的坐标，利用向量的坐标运算求出
+
的坐标，由①和向量的模列出关系式，化简后可得到点P的轨迹方程，其轨迹方程为一个圆，找出圆心坐标和半径，根据平面几何知识即可得到|PQ|的最大值及最小值．
| PA |
| PB |
解答：解：根据②③画出图形如下：并以AB 为x轴，以AQ为y轴建立坐标系，
∵|
+
|=|
-
|，∴|
|=|
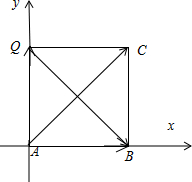
|，则四边形ABCQ是矩形，
∵(
+
)•
=0，∴AC⊥BQ，则四边形ABCQ是正方形，
则A（0，0），B（2，0），Q（0，2），C（2，2），设P（x，y），
∴
+
=（-x，-y）+（2-x，-y）=（2-2x，-2y），
∵|
+
|=|
|=2，∴（2-2x）2+4y2=4，化简得（x-1）2+y2=1，
则点P得轨迹是以（1，0）为圆心，以1为半径的圆，
∴|PQ|是点Q（0，2）到圆（x-1）2+y2=1任一点的距离，
则|PQ|最大值是
+1，最小值是
-1，
即|
|的最大值与最小值之差是2，
故答案为2．
∵|
| AB |
| AQ |
| AB |
| AQ |
| AC |
| QB |
∵(
| ||
|
|
| ||
|
|
| BQ |
则A（0，0），B（2，0），Q（0，2），C（2，2），设P（x，y），
∴
| PA |
| PB |
∵|
| PA |
| PB |
| AB |
则点P得轨迹是以（1，0）为圆心，以1为半径的圆，
∴|PQ|是点Q（0，2）到圆（x-1）2+y2=1任一点的距离，
则|PQ|最大值是
| 5 |
| 5 |
即|
| PQ |
故答案为2．
点评：本题题考查了向量的线性运算的几何意义，数量积的性质，以及圆的标准方程和两点间的距离公式，解本题的关键是根据题意正确画出图形，并判断出特征，再建立合适的平面直角坐标系，找出动点P的轨迹方程，难度较大，体现了向量问题、几何问题和代数问题的转化．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
（2013•浙江模拟）函数f（x）=Asin（ωx+φ）（A＞0，ω＞），|φ|＜
（2013•浙江模拟）如图，在四边形ABCD中，AB⊥BC，AD⊥DC．若|