题目内容
13.已知:sinα=$\frac{1}{5}$且tanα<0,试用定义求α的其余三个三角函数值.分析 直接利用同角三角函数的基本关系式求解函数值即可.
解答 解:sinα=$\frac{1}{5}$且tanα<0,可知α是第二象限角.
cosα=-$\sqrt{1-{sin}^{2}α}$=-$\frac{2\sqrt{5}}{5}$.
tanα=$\frac{sinα}{cosα}$=-2.
cot$α=-\frac{1}{2}$.
点评 本题考查同角三角函数的基本关系式的应用,考查计算能力.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
3.函数f(x)=[x]的函数值表示不超过x的最大整数,例如[-3.5]=-4,[2.1]=2,则函数f(x)=[x],x∈[-2,3]与直线y=x(x∈R)的交点个数( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
2.下面几个空间图形中,虚线、实线使用不正确的有( )
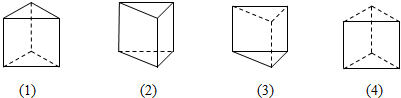

| A. | (2)(3) | B. | (1)(3) | C. | (3)(4) | D. | (4) |
3. 如图是一个程序框图,则输出的n的值是( )
如图是一个程序框图,则输出的n的值是( )
 如图是一个程序框图,则输出的n的值是( )
如图是一个程序框图,则输出的n的值是( )| A. | 3 | B. | 5 | C. | 7 | D. | 9 |