题目内容
规定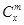 =
=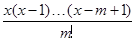 ,其中
,其中 是正整数,且
是正整数,且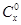 =1,这是组合数
=1,这是组合数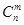 (
(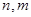 是正整数,且
是正整数,且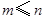 )的一种推广.
)的一种推广.
(1)求 的值;
的值;
(2)设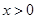 ,当
,当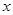 为何值时,
为何值时,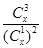 取得最小值?
取得最小值?
(3)组合数的两个性质:①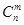 =
=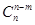 ; ②
; ②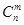 +
+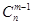 =
=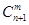
是否都能推广到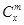 (
( 是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
是正整数)的情形?若能推广,则写出推广的形式并给出证明;若不能,则说明理由.
(1)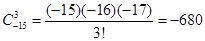 .
.
(2)当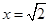 时,
时,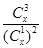 取得最小值.
取得最小值.
(3)性质①不能推广.例如当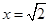 时,
时,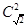 有意义,但
有意义,但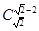 无意义;
无意义;
性质②能推广,其推广形式是: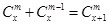 ,
, 是正整数,
是正整数,
解析试题分析:(1)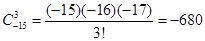 . 4分
. 4分
(2)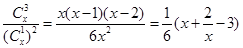
∵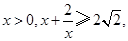 当且仅当
当且仅当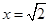 时,取等号
时,取等号
∴当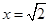 时,
时,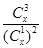 取得最小值. 8分
取得最小值. 8分
(3)性质①不能推广.例如当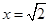 时,
时,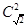 有意义,但
有意义,但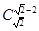 无意义;
无意义;
性质②能推广,其推广形式是: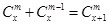 ,
, 是正整数,12分
是正整数,12分
事实上,当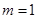 时,有
时,有 ,
,
当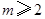 时,
时,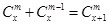
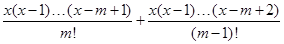
=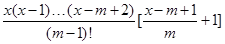
= . 15分
. 15分
考点:本题主要考查组合数的性质及其应用,归纳推理,均值定理的应用。
点评:中档题,本题由3道小题组成,前两小题解题思路明确,利用组合数公式及其性质变形、计算,其中(2)在得到函数表达式的基础上,灵活运用均值定理求最值,具有一般性。(3)利用归纳推理,作出判断,利用组合数公式及其性质进行了证明,对复杂式子变形能力要求高。

练习册系列答案
相关题目
 的展开式的二项式系数和比
的展开式的二项式系数和比 的展开式的系数和大992,求
的展开式的系数和大992,求 的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。
的展开式中:①二项式系数最大的项;②系数的绝对值最大的项。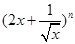 的展开式前两项的二项式系数的和为10.
的展开式前两项的二项式系数的和为10.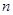 的值.
的值. 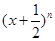 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.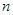 的值;(2)设
的值;(2)设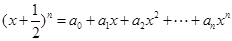 .
.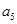 的值; ②求
的值; ②求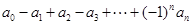 的值.
的值. (
(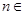 N*)展开式中,前三项的二项式系数和是
N*)展开式中,前三项的二项式系数和是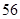 ,求:
,求: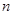 的值;
的值;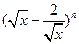 二项展开式中,第4项的二项式系数与第3项的二项式系数的比为
二项展开式中,第4项的二项式系数与第3项的二项式系数的比为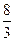 .
.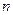 的值;
的值;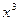 项的系数。
项的系数。