题目内容
9.曲线$f(x)=\frac{xlnx}{e^x}$在点(1,f(1))处的切线方程为x-ey-1=0.分析 求得f(x)的导数,可得在x=1处的切线的斜率,求得切点,由点斜式方程可得切线的方程.
解答 解:$f(x)=\frac{xlnx}{e^x}$的导数为
$f'(x)=\frac{lnx+1-xlnx}{e^x}$,
可得在点(1,f(1))处的切线斜率为$f'(1)=\frac{1}{e}$,
又f(1)=0,
故切线方程为$y=\frac{1}{e}(x-1)$,
即为x-ey-1=0.
故答案为:x-ey-1=0.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,正确求导和运用直线的点斜式方程是解题的关键,属于基础题.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
17.已知a,b∈R,函数f(x)=ax-b,若对任意x∈[-1,1],有0≤f(x)≤1,则$\frac{3a+b+1}{a+2b-2}$的取值范围为( )
| A. | [-$\frac{1}{2}$,0] | B. | [-$\frac{4}{5}$,0] | C. | [-$\frac{1}{2}$,$\frac{2}{7}$] | D. | [-$\frac{4}{5}$,$\frac{2}{7}$] |
4.某商店经营一批进价为每千克3.5元的商品,调查发现,此商品的销售单价x(元/千克)与日销量y(千克)之间有如下关系:
若x与y具有线性相关关系y=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,且$\stackrel{∧}{b}$=-2.6为使日销售利润最大,则销售单价应定为(结果保留一位小数)( )
| x | 5 | 6 | 7 | 8 |
| y | 20 | 17 | 15 | 12 |
| A. | 7.5 | B. | 7.8 | C. | 8.1 | D. | 8.4 |
19.已知数列{logabn}(a>0且a≠1)是首项为2,公差为1的等差数列,若数列{an}是递增数列,且满足an=bnlgbn,则实数a的取值范围是( )
| A. | ($\frac{2}{3}$,1) | B. | (2,+∞) | C. | ($\frac{2}{3}$,1)∪(1,+∞) | D. | (0,$\frac{2}{3}$)∪(1,+∞) |
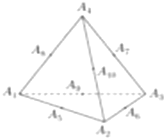 已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.
已知正四面体A1A2A3A4,点A5,A6,A7,A8,A9,A10分别是所在棱的中点,如图,则当1≤i≤10,1≤j≤10,且i≠j时,数量积$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{i}{A}_{j}}$的不同数值的个数为9.