题目内容
(本题10分)某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30min抽取一包产品,称其重量,分别记录抽查数据如下:
甲:102, 101, 99, 98, 103, 98, 99;
乙:110, 115, 90, 85, 75, 115, 110。
(Ⅰ)这种抽样方法叫做什么抽样方法?
(Ⅱ)将这两组数据用茎叶图表示出来;
(Ⅲ)将两组数据比较:说明哪个车间的产品较稳定。
(Ⅰ)因间隔时间相同,故是系统抽样。
(Ⅱ)茎叶图如下:
(Ⅲ) 。
。
解析试题分析:(Ⅰ)因间隔时间相同,故是系统抽样。 …………………………2分
(Ⅱ)茎叶图如下: …………6分
…………6分
(Ⅲ)甲车间:
平均值: (102+101+99+98+103+98+99)=100
(102+101+99+98+103+98+99)=100
方差:
乙车间:
平均值: (100+115+90+85+75+115+110)=100
(100+115+90+85+75+115+110)=100
方差:
 ,
,  。 …………………………………10分
。 …………………………………10分
考点:本题主要考查抽样方法,茎叶图,平均数,方差的计算。
点评:基础题,茎叶图形象直观,易于操作,原始数据保留完好。确定产品的稳定性优劣,一般先计算平均数,相同情况下,计算方差,根据离散程度确定。

(本题满分12分)
对某校高二年级学生参加社会实践活动次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践活动的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
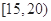 | 26 | n |
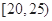 | m | P |
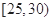 | 1 | 0.025 |
| 合计 | M | 1 |
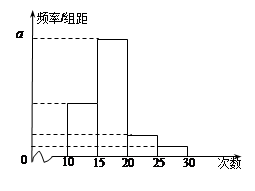
(Ⅰ)求出表中M,P及图中
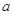 的值;
的值;(Ⅱ)在所取样本中,从参加社会实践活动的次数不少于20次的学生中任选2人,求恰有一人参加社会实践活动次数在区间
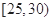 内的概率.
内的概率. 某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程
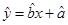 ;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。
;(3)试根据(II)求出的线性回归方程,预测记忆力为9的同学的判断力。(相关公式:
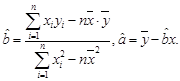 )
) 电视传媒公司为了解某地区观众对某类体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名。下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:
将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.
(Ⅰ)根据已知条件完成下面的2×2列联表,并据此资料判断是否有95%的把握认为“体育迷”与性别有关?
| | 非体育迷 | 体育迷 | 合计 |
| 男 | | | |
| 女 | | | |
| 合计 | | | |
附:K2=
 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(本题满分10分)对某校高三年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
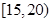 | 24 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 |  | 1 |

(Ⅰ)求出表中
 及图中
及图中 的值;
的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
 内的人数;
内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
 内的概率.
内的概率.  .
.
 分内的人数.
分内的人数.

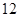 名男志愿者和
名男志愿者和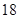 名女志愿者,调查发现,这
名女志愿者,调查发现,这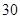 名志愿者的身高如下:(单位:cm )
名志愿者的身高如下:(单位:cm )
 cm以上(包括
cm以上(包括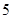 人,再从这
人,再从这 人,则至少有一人是“高个子”的概率是多少?
人,则至少有一人是“高个子”的概率是多少?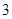 名志愿者,用
名志愿者,用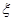 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出