Question

【题目】已知定义在R上的函数是奇函数.

（1）求实数a，b的值；

（2）若对任意实数x，不等式f（4x﹣k2x）+f（22x+1﹣k）＜0恒成立，求实数k的取值范围.

Answer 1

【答案】（1）a＝2，b＝1（2）（﹣∞，0]

【解析】

（1）根据奇函数的必要条件，利用，求出值，再用奇函数的定义证明；

（2）恒成立，由已知转化为

恒成立，利用在单调递减，原不等式转为恒成立，换元令，转化为恒成立，设，只需求出，即可求出结论.

定义在R上的函数是奇函数，

由.f（0）＝0，可得b＝1.

由f（﹣1）＝﹣f（1），即，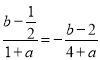

解得a＝2.∴f（x），

.

故得实数a＝2，b＝1.

（2）由，

∵y＝2x+1在上单调递增且，∴f（x）在上单调递减；

那么不等式f（4x﹣k2x）＜﹣f（22x+1﹣k）恒成立，

∵f（x）是奇函数，又是递减函数；

则，

可得恒成立，

令t＝2x，（t＞0）

则恒成立，

若，则，可得成立；

若，则，即，此时无解

综上实数k的取值范围.