题目内容
若函数f(x)在定义域R内可导,f(2+x)=f(2-x),且当x∈(-∞ ,2)时,(x-2)
,2)时,(x-2)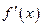 >0.设a=f(1
>0.设a=f(1 ),
),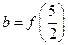 ,c=f(4),则a,b,c的大小为 .
,c=f(4),则a,b,c的大小为 .
 ,2)时,(x-2)
,2)时,(x-2)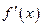 >0.设a=f(1
>0.设a=f(1 ),
),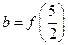 ,c=f(4),则a,b,c的大小为 .
,c=f(4),则a,b,c的大小为 .c>a>b
由f(2+x)=f(2-x)可得函数f(x)的对称轴为x=2,故a=f (1)=f(3),
(1)=f(3),
c=f(4),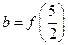 .
.
又由x∈(-∞,2)时,(x-2)f′(x)>0,可知f′(x)<0,即f(x)在(-∞,2)上是减函数,所以f(x)在(2,+∞)上是增函数于是f(4)>f(3)>f( ),即c>a>b.
),即c>a>b.
 (1)=f(3),
(1)=f(3),c=f(4),
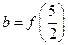 .
.又由x∈(-∞,2)时,(x-2)f′(x)>0,可知f′(x)<0,即f(x)在(-∞,2)上是减函数,所以f(x)在(2,+∞)上是增函数于是f(4)>f(3)>f(
 ),即c>a>b.
),即c>a>b.
练习册系列答案
相关题目
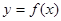 的导函数
的导函数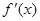 的图象,则下面判断正确的是( )
的图象,则下面判断正确的是( )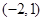 上
上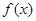 是增函数
是增函数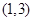 上
上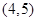 上
上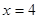 时,
时,
 求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4;
求证:对于区间[-1,1]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤4; 数
数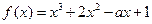 .
.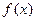 在点
在点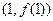 处的切线斜率为4,求实
处的切线斜率为4,求实 数
数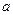 的值;
的值;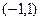 上是单调函数,求实数
上是单调函数,求实数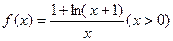
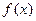 在区间
在区间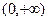
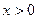 时,
时,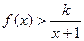 恒成立,求正整数
恒成立,求正整数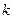 的最大值。
的最大值。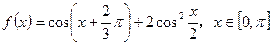 。
。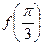 的值;
的值; 的最小值及
的最小值及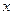 的集合;(3)求
的集合;(3)求
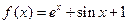 在
在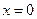 处的切线方程为
处的切线方程为 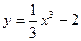 以点(1,-
以点(1,-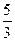 )为切点的切线的倾斜角为
)为切点的切线的倾斜角为