题目内容
12．不等式（$\frac{1}{3}$）1-x＜7的解集为（-∞，log321）．分析 根据指数幂的运算法则，和对数的定义，即可求出不等式的解集．
解答 解：∵（$\frac{1}{3}$）1-x＜7，
∴3x-1＜7，
两边取以3为底的对数得，
x-1＜log37，
∴x＜1+log37=log321，
故不等式的解集为（-∞，log321），
故答案为：（-∞，log321）．
点评 本题考查了幂的运算法则和对数的定义，以及不等式的解法，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
7．已知集合M={f（x）|f（x）=$\frac{1}{\sqrt{1-x}}$}，N={g（x）|g（x）=ln（x+1）}，则M∩N=（ ）
| A． | （1，1） | B． | （0，+∞） | C． | （1，+∞） | D． | （-∞，1） |
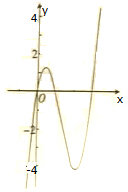已知函数f（x）=2x（x-1）（x-3）的图象如图所示，有以下关于方程f（x）+1=0的说法：①有2个实数根；②当x＞0时，有1个实数根；③当-1＜x＜0时，有1个实数根；④当x＞1时，有1个实数根；⑤当-1＜x＜3时，有3个实数根．其中正确说法的序号是③⑤（填上所有正确命题的序号）．