题目内容
已知函数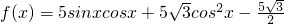 ;
;
(Ⅰ)确定函数f(x)的单调增区间;
(Ⅱ)当函数f(x)取得最大值时,求自变量x的集合.
解:(Ⅰ)由题意知,
= .
.
由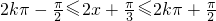 解得,
解得,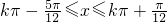 ,(k∈z)
,(k∈z)
∴f(x) 的单调增区间为 .
.
(Ⅱ)由(Ⅰ)知, ,
,
当 时,即
时,即 时,f(x)max=5,
时,f(x)max=5,
此时自变量x的集合是{x| }.
}.
分析:(Ⅰ)根据两角和的正弦公式将解析式化为 ,再根据正弦函数的增区间,求出函数的增区间;
,再根据正弦函数的增区间,求出函数的增区间;
(Ⅱ)根据(I)和正弦函数的最大值,令 求x的表达式,即所求的集合.
求x的表达式,即所求的集合.
点评:本题考查了形如y=sin(ωx+φ)的函数性质,主要利用两角和、差的正弦公式对解析式进行化简,利用“整体思想”和正弦函数的性质进行求解.

=
 .
. 由
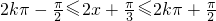 解得,
解得,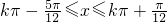 ,(k∈z)
,(k∈z)∴f(x) 的单调增区间为
 .
.(Ⅱ)由(Ⅰ)知,
 ,
,当
 时,即
时,即 时,f(x)max=5,
时,f(x)max=5,此时自变量x的集合是{x|
 }.
}.分析:(Ⅰ)根据两角和的正弦公式将解析式化为
 ,再根据正弦函数的增区间,求出函数的增区间;
,再根据正弦函数的增区间,求出函数的增区间;(Ⅱ)根据(I)和正弦函数的最大值,令
 求x的表达式,即所求的集合.
求x的表达式,即所求的集合.点评:本题考查了形如y=sin(ωx+φ)的函数性质,主要利用两角和、差的正弦公式对解析式进行化简,利用“整体思想”和正弦函数的性质进行求解.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
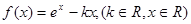
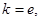 试确定函数
试确定函数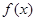 的单调区间;
的单调区间;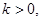 且对于任意
且对于任意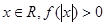 恒成立,试确定实数
恒成立,试确定实数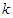 的取值范围;
的取值范围; 求证:
求证: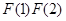
 .
.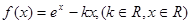
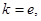 试确定函数
试确定函数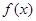 的单调区间;
的单调区间;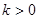 ,且对于任意
,且对于任意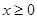 ,
,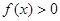 恒成立,求实数
恒成立,求实数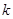 的取值范围;
的取值范围;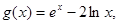 若至少存在一个实数
若至少存在一个实数 ,使
,使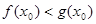 成立,求实数
成立,求实数
 ,试确定a、b的值,使f(x)在x=0处可导.
,试确定a、b的值,使f(x)在x=0处可导.
 的范围,使得函数
的范围,使得函数 在
在 上是单调函数;
上是单调函数; 上的最值.
上的最值.