题目内容
11.若空间向量$\overrightarrow{a}$=(1,-1,0),$\overrightarrow{b}$=(-1,2,1),$\overrightarrow{c}$=(2,1,m)共面,则m=3.分析 空间向量$\overrightarrow{a}$=(1,-1,0),$\overrightarrow{b}$=(-1,2,1),$\overrightarrow{c}$=(2,1,m)共面,可得:存在实数λ,μ使得$\overrightarrow{c}=λ\overrightarrow{a}+μ\overrightarrow{b}$,利用向量的线性运算与向量相等即可得出.
解答 解:∵空间向量$\overrightarrow{a}$=(1,-1,0),$\overrightarrow{b}$=(-1,2,1),$\overrightarrow{c}$=(2,1,m)共面,
∴存在实数λ,μ使得$\overrightarrow{c}=λ\overrightarrow{a}+μ\overrightarrow{b}$,
∴$\left\{\begin{array}{l}{2=λ-μ}\\{1=-λ+2μ}\\{m=μ}\end{array}\right.$,解得m=3.
故答案为:3.
点评 本题考查了向量共面定理、向量的线性运算与向量相等,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.在△ABC中,点D在线段BC上,∠BAC=∠ADC,AC=8,BC=16,则CD为( )
| A. | 3 | B. | 6 | C. | 5 | D. | 4 |
3.下列说法正确的是( )
| A. | a2>b2是a>b的必要条件 | |
| B. | “若a∈(0,1),则关于x的不等式ax2+2ax+1>0解集为R”的逆命题为真 | |
| C. | “若a,b不都是偶数,则a+b不是偶数”的否命题为假 | |
| D. | “已知a,b∈R,若a+b≠3,则a≠2或b≠1”的逆否命题为真 |
1.直线y=a分别与曲线y=3x+2,y=2x+Inx交于A,B两点,则|AB|的最小值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
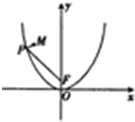 已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.
已知抛物线C:x2=2y的焦点为F,P为抛物线C上的任意一点,点M(-2,3),则|MP|+|PF|的最小值为$\frac{7}{2}$.