题目内容
14.求(1-x)6(1+x)4展开式中x3的系数.分析 利用二项展开式的通项公式求出通项,再利用多项式的乘法进一步求x3的系数.
解答 解:(1-x)6,(1-x)4的通项公式分别为Tr+1=(-1)rC6rxr,Tr+1=C4rxr,
从而x3的系数是1×4-6×6+15×4-20=8.
点评 本题考查二项式系数的性质,关键是根据多项式的运算法则合理地进行等价转化,是基础题.

练习册系列答案
相关题目
2.曲线y=$\frac{1}{2}$x2-2x在x=3处的切线的倾斜角为( )
| A. | 45° | B. | -45° | C. | 135° | D. | -135° |
1.已知a,b为异面直线,下列结论不正确的是( )
| A. | 必存在平面α使得a∥α,b∥α | |
| B. | 必存在平面α使得a,b与α所成角相等 | |
| C. | 必存在平面α使得a?α,b⊥α | |
| D. | 必存在平面α使得a,b与α的距离相等 |
2.已知数列{an}的前n项和为Sn,若Sn=2an-4,n∈N*,则an=( )
| A. | 2n+1 | B. | 2n | C. | 2n-1 | D. | 2n-2 |
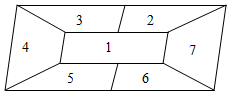 巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.
巴蜀中学的“开心农场”有一如图所示的7块地方,现准备在这7块地方种植不同的植物,要求相邻地方不能种同一植物,现在只有4种不同的植物可供选择,每种植物有足量的数量,恰好把4种不同植物都用上的不同种植方法有576种.