题目内容
设偶函数f(x)的定义域为R,当x 时f(x)是增函数,则f(-2),f(
时f(x)是增函数,则f(-2),f( ),f(-3)的大小关系是:( )
),f(-3)的大小关系是:( )
A.f( )>f(-3)>f(-2) )>f(-3)>f(-2) | B.f( )>f(-2)>f(-3) )>f(-2)>f(-3) |
C.f( )<f(-3)<f(-2) )<f(-3)<f(-2) | D.f( )<f(-2)<f(-3) )<f(-2)<f(-3) |
A
解析试题分析:∵函数f(x)是在[0,+∞)上单调递增的偶函数,∴ f(-2)=f(2)<f(3)=f(-3)< f( ),故选A
),故选A
考点:本题考查了函数性质的运用
点评:对于抽象函数值比较大小问题,往往利用奇偶性把自变量转化为同一个单调区间上处理,解题的关键是判断抽象函数的单调性

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
已知函数 ,,则函数
,,则函数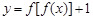 的零点个数是
的零点个数是
| A.4 | B.3 | C.2 | D.1 |
函数y= 的定义域为( )
的定义域为( )
A.(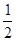 ,+∞) ,+∞) | B.[1,+∞ | C.( 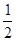 ,1 ,1 | D.(-∞,1)) |
函数 在区间
在区间 单调递增,则实数
单调递增,则实数 的取值范围为
的取值范围为
A. | B. | C. | D. |
若 ,则
,则 ( )
( )
| A.2 | B.4 | C. | D.10 |
若方程 的根在区间
的根在区间 上,则
上,则 的值为( )
的值为( )
A. | B.1 |
C. 或2 或2 | D. 或1 或1 |
若对任意的 ,函数
,函数 满足
满足 ,且
,且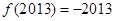 ,则
,则 ( )
( )
| A.0 | B.1 | C.-2013 | D.2013 |
设偶函数 满足
满足
 ,则
,则 ( )
( )
A. | B. |
C. | D. |
 ,若存在常数C,对任意的
,若存在常数C,对任意的 ,存在唯一的
,存在唯一的 ,使得
,使得 ,则称函数
,则称函数 在D上的几何平均数为C.已知
在D上的几何平均数为C.已知 ,则函数
,则函数 在
在 上的几何平均数为( )
上的几何平均数为( ) B.
B. C.
C. D.
D.