题目内容
已知向量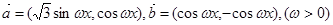 ,函数
,函数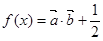 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为 .
.
(1)求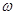 的值;
的值;
(2)若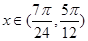 ,
,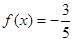 ,求
,求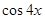 的值;
的值;
(3)若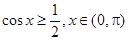 ,且
,且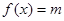 有且仅有一个实根,求实数
有且仅有一个实根,求实数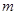 的值.
的值.
(1)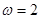 ;(2)
;(2)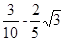 ;(3)
;(3) .
.
解析试题分析:(1)根据数量积公式将 进行化简,得到
进行化简,得到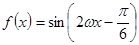 ,两相邻对称轴之间的距离为半个周期,所以根据周期公式
,两相邻对称轴之间的距离为半个周期,所以根据周期公式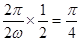 ,得到
,得到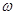 的值;
的值;
(2)根据第一问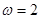 ,可得
,可得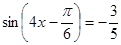 ,所以
,所以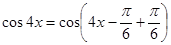 ,用已知角表示未知角,根据
,用已知角表示未知角,根据 的范围,求出
的范围,求出 的范围,最后求
的范围,最后求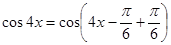 的值;
的值;
(3)画出 ,
,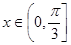 的图像,令
的图像,令 ,与其只有一个交点,即可求出
,与其只有一个交点,即可求出 的值.
的值.
解:由题意,
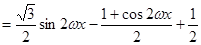

 ,
,
(1)∵两相邻对称轴间的距离为 ,
,
∴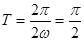 , ∴
, ∴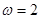 . 4分
. 4分
(2)由(1)得,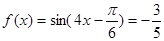 ,
,
∵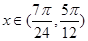 , ∴
, ∴ ,
,
∴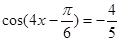 ,
,
∴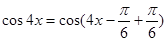

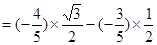
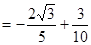 . 8分
. 8分
(3)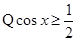 ,且余弦函数在
,且余弦函数在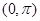 上是减函数, ∴
上是减函数, ∴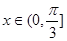 ,
,
令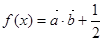 =
=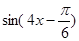 ,
,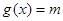 ,在同一直角坐标系中作出两个函数的图象,可知
,在同一直角坐标系中作出两个函数的图象,可知 . 13分
. 13分
考点:1.三角函数的化简求值;2.函数图像.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 +sin
+sin 的值;
的值; 的值.
的值.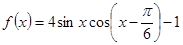 ,求函数
,求函数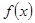 的最小正周期;
的最小正周期;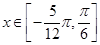 时,求函数
时,求函数
 的最小正周期;
的最小正周期; 时,求函数f(x)的单调区间。
时,求函数f(x)的单调区间。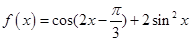 ,
,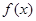 的最大值和最小正周期;
的最大值和最小正周期; 为锐角,且
为锐角,且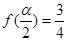 ,求
,求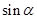 的值.
的值.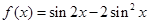
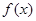 的最小正周期。
的最小正周期。 的内角
的内角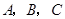 所对的边长分别为
所对的边长分别为 ,且
,且 ,A=
,A= ,
,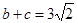 .
.
 的单调递增区间及最大值;
的单调递增区间及最大值;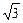 cosωx),其中0<ω<2,函数
cosωx),其中0<ω<2,函数 ,其图象的一条对称轴为
,其图象的一条对称轴为 。
。 ,b=1,
,b=1,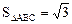 ,求a的值。
,求a的值。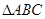 中,角
中,角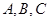 所对的边分别为
所对的边分别为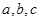 ,且满足
,且满足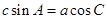 .
.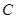 的大小;
的大小;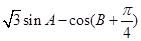 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角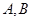 的大小.
的大小.