题目内容
抛物线y2=mx的焦点为F,点P(2,2 )在此抛物线上,M为线段PF的中点,则点M到该抛物线准线的距离为( )
)在此抛物线上,M为线段PF的中点,则点M到该抛物线准线的距离为( )A.1
B.

C.2
D.

【答案】分析:先确定抛物线的标准方程,求出抛物线的焦点坐标与准线方程,由此可求点P到该抛物线准线的距离为3,F到该抛物线准线的距离为2,从而可求点M到该抛物线准线的距离.
解答:解:∵点P(2,2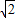 )在抛物线y2=mx
)在抛物线y2=mx
∴8=2m
∴m=4
∴抛物线方程为y2=4x
∴F(1,0),抛物线的准线方程为x=-1
∴点P到该抛物线准线的距离为3,F到该抛物线准线的距离为2
∵M为线段PF的中点,
∴点M到该抛物线准线的距离为
故选D.
点评:本题重点考查抛物线的标准方程,考查抛物线的定义,解题的关键是确定抛物线的方程.
解答:解:∵点P(2,2
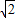 )在抛物线y2=mx
)在抛物线y2=mx∴8=2m
∴m=4
∴抛物线方程为y2=4x
∴F(1,0),抛物线的准线方程为x=-1
∴点P到该抛物线准线的距离为3,F到该抛物线准线的距离为2
∵M为线段PF的中点,
∴点M到该抛物线准线的距离为

故选D.
点评:本题重点考查抛物线的标准方程,考查抛物线的定义,解题的关键是确定抛物线的方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 )在此抛物线上,M为线段PF的中点,则点M到该抛物线准线的距离为
)在此抛物线上,M为线段PF的中点,则点M到该抛物线准线的距离为
