题目内容
【题目】已知椭圆 
，点P（ 
）在椭圆上．
（1）求椭圆的离心率；
（2）设A为椭圆的左顶点，O为坐标原点．若点Q在椭圆上且满足|AQ|=|AO|，求直线OQ的斜率的值．
【答案】
（1）解：因为点P（ 
）在椭圆上，所以 
∴ 
∴ 
∴ 
（2）解：设直线OQ的斜率为，则其方程为y=kx
设点Q的坐标为（x0，y0），由条件得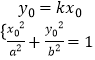 
，消元并整理可得 
①
∵|AQ|=|AO|，A（﹣a，0），y0=kx0，
∴ 
∴ 
∵x0≠0，∴ 
代入①，整理得 
∵
∴ 
+4，
∴5k4﹣22k2﹣15=0
∴k2=5
∴ 
【解析】（1）根据点P（ ）在椭圆上，可得 ，由此可求椭圆的离心率；（2）设直线OQ的斜率为k，则其方程为y=kx，设点Q的坐标为（x0 ， y0），与椭圆方程联立， ，根据|AQ|=|AO|，A（﹣a，0），y0=kx0 ， 可求 ，由此可求直线OQ的斜率的值．
练习册系列答案
相关题目
