Question

【题目】已知二次函数，关于实数的不等式的解集为．

（1）当时，解关于的不等式： ；

（2）是否存在实数，使得关于的函数（）的最小值为？若存在，求实数的值；若不存在，说明理由．

Answer 1

【答案】(1) 答案见解析；(2)存在满足条件的．

【解析】试题分析：

(1)由题意结合二次函数的性质分类讨论可得：

当时，原不等式解集为；

当时，原不等式的解集为；

当时，原不等式的解集为．

(2)假设存在满足条件的实数，结合（1）的结论，换元令，则， ，结合二次函数的性质讨论可得在满足条件的．

试题解析：

（1）由不等式的解集为知，

关于的方程的两根为-1和，且，

由根与系数关系，得， ∴，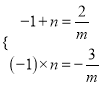

所以原不等式化为，

①当时，原不等式转化为，解得；

②当时，原不等式化为，且，解得或；

③当时，原不等式化为，解得且；

④当时，原不等式化为，且，

解得或；

综上所述：当时，原不等式解集为；

当时，原不等式的解集为；

当时，原不等式的解集为．

（2）假设存在满足条件的实数，

由（1）得： ，

，

令，则， ，

对称轴，

因为，所以， ，

所以函数在单调递减，

所以当时， 的最小值为，

解得（舍去），或，

故存在满足条件的．