题目内容
已知椭圆的左右焦点为F1,F2,过F1,F2作倾斜角都为45°的两条直线与椭圆交于四点,所构成的四边形与椭圆四个顶点所构成的四边形面积之比为
,则离心率 .
2
| ||
| 3 |
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:设椭圆的方程为
+
=1,过F1且倾斜角是45度的一条直线方程是y=x+c,联立化简求|y1-y2|=2
,从而求以该四点为顶点的四边形的面积S1=|F1F2||y1-y2|=2c2
;再求以椭圆的四个顶点为顶点的四边形的面积是S2=2ab;从而得到比值,化简可得离心率.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| ab2 |
| a2+b2 |
| 2 |
| ab2 |
| a2+b2 |
解答:
解:设椭圆的方程为
+
=1,过F1且倾斜角是45度的一条直线方程是y=x+c,
代入到椭圆方程化简可得,
(a2+b2)y2-2b2cy-b4=0,
y1+y2=
,y1y2=
;
(y1-y2)2=(
)2-4
=
;
|y1-y2|=2
,
故以该四点为顶点的四边形的面积S1=|F1F2||y1-y2|=2c2
;
以椭圆的四个顶点为顶点的四边形的面积是S2=2ab;
又∵
=
,
2b2+c2=3bc;
(2b-c)(b-c)=0,
2b=c或b=c;
a2=b2+4b2=5b2或a2=2b2,
故a=
b或a=
b;
又∵e=
,
∴e=
或
.
故答案为:
或
.
| x2 |
| a2 |
| y2 |
| b2 |
代入到椭圆方程化简可得,
(a2+b2)y2-2b2cy-b4=0,
y1+y2=
| 2b2c |
| a2+b2 |
| -b4 |
| a2+b2 |
(y1-y2)2=(
| 2b2c |
| a2+b2 |
| -b4 |
| a2+b2 |
| 8a2b4 |
| (a2+b2)2 |
|y1-y2|=2
| 2 |
| ab2 |
| a2+b2 |
故以该四点为顶点的四边形的面积S1=|F1F2||y1-y2|=2c2
| 2 |
| ab2 |
| a2+b2 |
以椭圆的四个顶点为顶点的四边形的面积是S2=2ab;
又∵
| S1 |
| S2 |
2
| ||
| 3 |
2b2+c2=3bc;
(2b-c)(b-c)=0,
2b=c或b=c;
a2=b2+4b2=5b2或a2=2b2,
故a=
| 5 |
| 2 |
又∵e=
| c |
| a |
∴e=
2
| ||
| 5 |
| ||
| 2 |
故答案为:
2
| ||
| 5 |
| ||
| 2 |
点评:本题考查了圆锥曲线与直线的位置关系应用,属于中档题.

练习册系列答案
相关题目
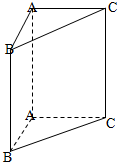 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=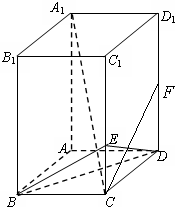 如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,BB1=4,E是棱CC1上的点,且CE=1;F是DD1中点
如图所示,在长方体ABCD-A1B1C1D1中,AB=BC=2,BB1=4,E是棱CC1上的点,且CE=1;F是DD1中点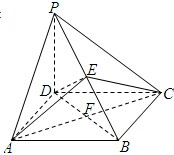 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6