题目内容
已知数列![]() 满足
满足![]() ,且
,且![]() .试猜想
.试猜想![]() 的最小值,使得
的最小值,使得![]() 对
对![]() 恒成立,并给出证明.
恒成立,并给出证明.
解:当n=1时,![]() ,因为
,因为![]() ,所以欲
,所以欲![]() 恒成立,
恒成立,
则要 恒成立,解得
恒成立,解得![]() ,由此猜想
,由此猜想![]() 的最小值为2………………………………4分
的最小值为2………………………………4分
因为![]() ,所以要证该猜想成立,只要证:当
,所以要证该猜想成立,只要证:当![]() 时,
时,![]() 对
对![]() 恒成立…………………5分
恒成立…………………5分
现用数学归纳法证明之:①当n=1时结论显然成立.……………………………………………………6分
②假设当n=k时结论成立,即ak∈(0, 2),
则当n=k+1时,ak+1=-ak2+2ak= ak(2-ak)
一方面,ak+1=ak(2-ak)>0成立………………………………………………………………………… 8分
另一方面,ak+1=ak(2-ak)=-(ak-1)2+1≤1<2,所以ak+1∈(0, 2),即当n=k+1时结论也成立.… 9分
由①、②可知,猜想成立,即![]() 的最小值为2……………………………………………………………10分
的最小值为2……………………………………………………………10分

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
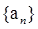 满足:
满足: ,
,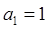 ,
, 为公差为4等差数列.数列
为公差为4等差数列.数列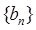 的前n项和为
的前n项和为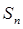 ,且满足
,且满足
 .
.
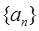 的通项公式
的通项公式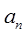 ;
; 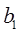 的值,使得数列
的值,使得数列 是等差数列;
是等差数列; 满足:
满足: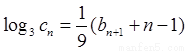
 与
与 之间插
之间插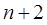 个数组成一个公差为
个数组成一个公差为 的等差数列.
的等差数列. 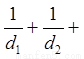 ……
…… 。
。 满足
满足 且
且
 ;
; 满足
满足 ,且
,且 时
时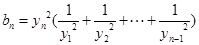 .证明当
.证明当 时,
时,  ;
; 与4的大小关系.
与4的大小关系. 满足
满足 且
且
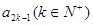 ;
; 满足
满足 ,且
,且 时
时 .
. 时,
时,  ;
; 与4的大小关系.
与4的大小关系.