题目内容
已知数列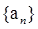 满足:
满足: ,
,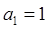 ,
, 为公差为4等差数列.数列
为公差为4等差数列.数列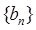 的前n项和为
的前n项和为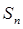 ,且满足
,且满足
 .
.
①求数列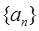 的通项公式
的通项公式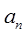 ;
;
②试确定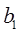 的值,使得数列
的值,使得数列 是等差数列;
是等差数列;
③设数列 满足:
满足: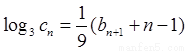
 ,若在
,若在 与
与 之间插
之间插
入n个数,使得这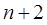 个数组成一个公差为
个数组成一个公差为 的等差数列.
的等差数列.
求证: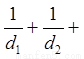 ……
…… 。
。
【答案】
① ②1③见解析
②1③见解析
【解析】本试题主要是考查了等差数列的通项公式的运用以及数列求和中错位相减法的综合运用。
(1)因为 为公差为4等差数列.∴
为公差为4等差数列.∴
∵ ∴
∴ 可知其通项公式。
可知其通项公式。
(2)
由
得到 ,分析数列
,分析数列
(3)由上可知

故 ,利用裂项求和的思想得到结论。
,利用裂项求和的思想得到结论。
解:①∵ 为公差为4等差数列.∴
为公差为4等差数列.∴
∵ ∴
∴ ∴
∴
∵ ∴
∴ .………………4分
.………………4分
②  ,
,
得 ,…………6分
,…………6分
∴ ∴
∴
∴ …………………7分
…………………7分
若 为等差数列,则
为等差数列,则
∴ ……………………8分
……………………8分
③依题意 =
= ,
,
∴  ,……………………8分
,……………………8分
则 ,由题知:
,由题知:
 ,则
,则 .……………10分
.……………10分
由上知: ,
,
所以
 ,
,
所以 …………12分
…………12分
 ,
,
所以 .……………………14分
.……………………14分

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
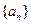 满足:
满足: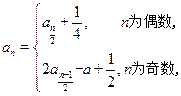 (
(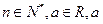 为常数),数列
为常数),数列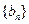 中,
中,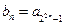 。
。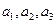 ;
;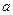 为有理数。
为有理数。 满足
满足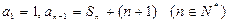 ,其中
,其中 为
为 项和,
项和,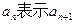 ;
;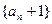 是等比数列;
是等比数列;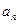 和
和 满足
满足 前
前 项和为
项和为 ,
,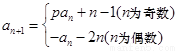 .
. 满足
满足 ,试求数列
,试求数列 ;
;  满足
满足 ,试判断
,试判断 ,求证:
,求证: ,不等式
,不等式 都成立,求
都成立,求 的取值范围.
的取值范围. 满足
满足 前
前 项和为
项和为 ,
, .
. 满足
满足 ,试求数列
,试求数列 ;(4分)
;(4分) 满足
满足 ,试判断
,试判断 时,问是否存在
时,问是否存在 ,使得
,使得 ,若存在,求出所有的
,若存在,求出所有的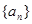 满足
满足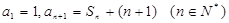 ,其中
,其中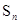 为
为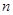 项和,
项和,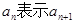 ;
;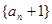 是等比数列;
是等比数列; 和
和