题目内容
设f(x)=(1)f′(x);
(2)f(x)图象在点(8,![]() )处的切线方程.
)处的切线方程.
解:(1)f′=(![]() )′
)′
=[(![]() )
)![]() ]′
]′
=![]() (
(![]() )
)![]() ·(
·(![]() )′
)′
=![]() (
(![]() )
)![]()
![]()
=![]() (
(![]() )
)![]()
![]()
=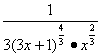
=![]() (3x+1)
(3x+1)![]() ·x
·x![]() .
.
(2)所求切线的斜率为k=f′(8)=![]() (3×8+1)
(3×8+1)![]() ·8
·8![]() =
=![]() ×25
×25![]() ·8
·8![]() =
=![]() ,所以切线方程为y-
,所以切线方程为y-![]() =
=![]() (x-8),即x-300
(x-8),即x-300![]() y+592=0.
y+592=0.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
设f(x)=(1)f′(x);
(2)f(x)图象在点(8,![]() )处的切线方程.
)处的切线方程.
解:(1)f′=(![]() )′
)′
=[(![]() )
)![]() ]′
]′
=![]() (
(![]() )
)![]() ·(
·(![]() )′
)′
=![]() (
(![]() )
)![]()
![]()
=![]() (
(![]() )
)![]()
![]()
=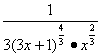
=![]() (3x+1)
(3x+1)![]() ·x
·x![]() .
.
(2)所求切线的斜率为k=f′(8)=![]() (3×8+1)
(3×8+1)![]() ·8
·8![]() =
=![]() ×25
×25![]() ·8
·8![]() =
=![]() ,所以切线方程为y-
,所以切线方程为y-![]() =
=![]() (x-8),即x-300
(x-8),即x-300![]() y+592=0.
y+592=0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案