题目内容
已知函数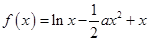 ,
,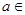 R.
R.
(1)求函数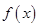 的单调区间;
的单调区间;
(2)是否存在实数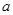 ,使得函数
,使得函数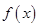 的极值大于
的极值大于 ?若存在,求
?若存在,求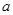 的取值范围;若不存
的取值范围;若不存
在,说明理由.
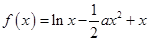 ,
,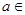 R.
R.(1)求函数
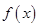 的单调区间;
的单调区间;(2)是否存在实数
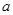 ,使得函数
,使得函数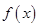 的极值大于
的极值大于 ?若存在,求
?若存在,求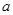 的取值范围;若不存
的取值范围;若不存在,说明理由.
(1)当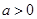 时,函数
时,函数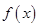 的单调递增区间为
的单调递增区间为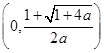 ,单调递减区间
,单调递减区间
为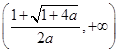 ;当
;当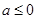 时,函数
时,函数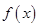 的单调递增区间为
的单调递增区间为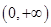 ,无单调递减区间. (2)存在,范围为
,无单调递减区间. (2)存在,范围为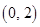
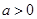 时,函数
时,函数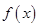 的单调递增区间为
的单调递增区间为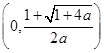 ,单调递减区间
,单调递减区间为
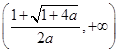 ;当
;当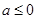 时,函数
时,函数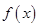 的单调递增区间为
的单调递增区间为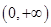 ,无单调递减区间. (2)存在,范围为
,无单调递减区间. (2)存在,范围为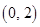
试题分析:(1)函数
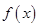 的定义域为
的定义域为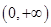 ,
,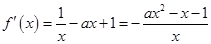 .
. ① 当
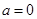 时,
时,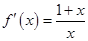 ,∵
,∵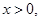 ∴
∴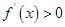 ,∴ 函数
,∴ 函数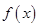 单调递增区间为
单调递增区间为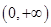
② 当
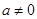 时,令
时,令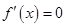 得
得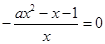 ,即
,即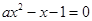 ,
,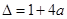 .
.(ⅰ)当
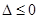 ,即
,即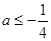 时,得
时,得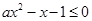 ,故
,故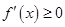 ,
,∴ 函数
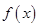 的单调递增区间为
的单调递增区间为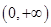 .
. (ⅱ)当
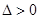 ,即
,即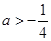 时,方程
时,方程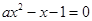 的两个实根分别为
的两个实根分别为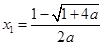 ,
,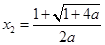 .
.若
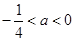 ,则
,则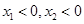 ,此时,当
,此时,当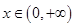 时,
时,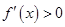 .
.∴函数
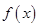 的单调递增区间为
的单调递增区间为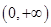 ,若
,若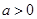 ,则
,则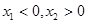 ,此时,当
,此时,当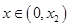 时,
时,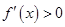 ,当
,当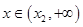 时,
时,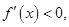
∴函数
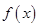 的单调递增区间为
的单调递增区间为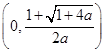 ,单调递减区间为
,单调递减区间为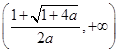 .
.综上所述,当
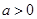 时,函数
时,函数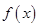 的单调递增区间为
的单调递增区间为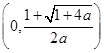 ,单调递减区间
,单调递减区间为
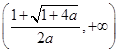 ;当
;当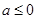 时,函数
时,函数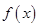 的单调递增区间为
的单调递增区间为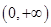 ,无单调递减区间.
,无单调递减区间.(2)由(1)得当
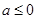 时,函数
时,函数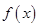 在
在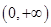 上单调递增,故函数
上单调递增,故函数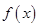 无极值
无极值 当
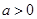 时,函数
时,函数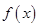 的单调递增区间为
的单调递增区间为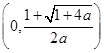 ,单调递减区间为
,单调递减区间为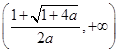 ,
,∴
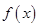 有极大值,其值为
有极大值,其值为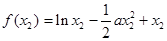 ,其中
,其中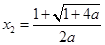 .
.∵
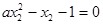 ,即
,即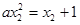 , ∴
, ∴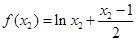 .
.设函数
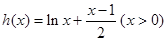 ,则
,则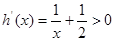 ,
,∴
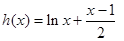 在
在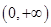 上为增函数,又
上为增函数,又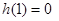 ,则
,则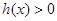
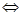
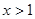 ,
,∴
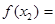
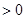
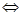
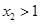 .
. 即
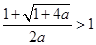 ,结合
,结合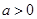 解得
解得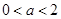 ,∴实数
,∴实数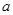 的取值范围为
的取值范围为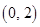 .
.点评:本题考查利用导数研究函数的单调性,利用导数研究函数的极值,突出分类讨论思想与转化思想的渗透与应用,属于难题,第二题把有正的极大值的问题转化为图象开口向下与X轴有两个交点,思路巧妙,学习中值得借鉴.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
 做函数
做函数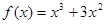 的切线,则切线方程为 。
的切线,则切线方程为 。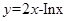 在点
在点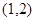 处的切线方程为( )
处的切线方程为( ) B.
B.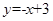 C.
C.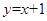 D.
D.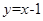
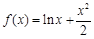 在区间
在区间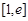 上的最大值是
上的最大值是 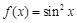 的导数是( )
的导数是( )
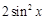

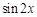
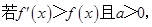 则
则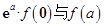 的大小关系为:
的大小关系为: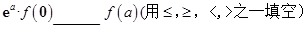
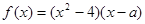
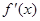 ;
;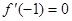 ,求
,求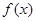 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值; 是自然对数底数,若函数
是自然对数底数,若函数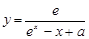 的定义域为
的定义域为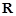 ,则实数
,则实数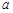 的取值范围为
的取值范围为

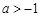
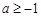
 ,已知
,已知 在
在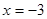 时取得极值,则
时取得极值,则 =
=