已知圆C关于直线x+y+2=0对称.且过点P和原点O．(1)求圆C的方程,(2)相互垂直的两条直线l1.l2都过点A.若l1.l2被圆C所截得弦长相等.求此时直线l1的方程．题目和参考答案——青夏教育精英家教网——

题目内容

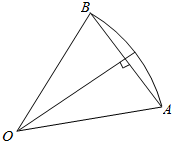
10．已知圆C关于直线x+y+2=0对称，且过点P（-2，2）和原点O．
（1）求圆C的方程；
（2）相互垂直的两条直线l₁，l₂都过点A（-1，0），若l₁，l₂被圆C所截得弦长相等，求此时直线l₁的方程．

分析（1）设圆心坐标为（a，-a-2），利用圆过点P（-2，2）和原点O，求出a，即可求圆C的方程；
（2）利用圆的对称性，直接求出直线的斜率，写出直线方程即可．

解答解：（1）设圆心坐标为（a，-a-2），则r²=（a+2）²+（-a-2-2）²=a²+（-a-2）²，
∴a=-2，r²=52，
∴圆C的方程为（x+2）²+y²=4；
（2）设圆C的圆心为C，l₁、l₂被圆C所截得弦长相等，
由圆的对称性可知，直线l₁的斜率k=±1，
∴直线l₁的方程为：x-y+1=0或x+y+1=0．

点评本题考查圆的标准方程的求法、直线和圆位置关系的综合应用，属于中档题．

练习册系列答案

Happy holiday欢乐假期暑假作业广东人民出版社系列答案

状元龙快乐学习暑假在线北方妇女儿童出版社系列答案

开拓者系列丛书高中新课标假期作业暑假作业内蒙古人民出版社系列答案

金牛系列高中新课标假期作业暑大众文艺出版社系列答案

石室金匮暑假作业电子科技大学出版社系列答案

学与练暑假生活宁夏人民教育出版社系列答案

优等生暑假作业云南人民出版社系列答案

快乐暑假暑假能力自测中西书局系列答案

志诚教育假期园地暑假作业中原农民出版社系列答案

快乐练习暑假衔接优计划晨光出版社系列答案

相关题目

20．已知数列{a_n}的前n项和为${S_n}={n^2}-2n$，则a₃+a₁₇=（　　）

1．为了解某班学生喜好体育运动是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
已知喜好体育运动与否，采用分层抽样法抽取容量为10的样本，则抽到喜好体育运动的人数为6．
（1）请将上面的列联表补充完整；
（2）能否在犯错误的概率不超过0.005的前提下认为喜好体育运动与性别有关？说明你的理由；

	喜好体育运动	不喜好体育运动	合计
男生		5
女生	10
合计			50

下面的临界值表供参考：

P（k₂≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式：K²=$\frac{n（ad-bc）^2}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

18．函数y=sin（x-$\frac{π}{3}$）的最小正周期为2π．

5．已知函数f（x）=sin（ωx+φ），ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$，相邻两对称轴间的距离为π，若将y=f（x）的图象向右平移$\frac{π}{6}$个单位，所得的函数y=g（x）为奇函数．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）若关于x的方程2[g（x）]²-m[g（x）]+1=0在区间[0，$\frac{π}{2}$]上有两个不相等的实根，求实数m的取值范围．

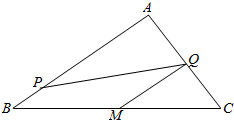如图，在Rt△ABC中，AB=4，AC=3，∠A=90°，$\overrightarrow{AP}$=m$\overrightarrow{PB}$，$\overrightarrow{AQ}$=n$\overrightarrow{QC}$，m，n＞0，且满足$\frac{1}{m}$+$\frac{1}{n}$=$\frac{1}{2}$，M是BC的中点，对任意的λ∈R，|λ•$\overrightarrow{QP}$+$\overrightarrow{QM}$|的最小值记为f（m），则对任意m＞0，f（m）的最大值为$\frac{1}{2}$．

2．若tanα+tanβ-tanαtanβ+1=0，α，β∈（$\frac{π}{2}，π$），则α+β=$\frac{7π}{4}$．

19．如图，已知扇形OAB的面积是4cm²，它的周长是8cm，求扇形的圆心角及弦AB的长．

20．（1-$\frac{3}{{x}^{3}}$）（x²+$\frac{2}{x}$）⁵的展开式中x⁴的系数为（　　）