题目内容
20.(1-$\frac{3}{{x}^{3}}$)(x2+$\frac{2}{x}$)5的展开式中x4的系数为( )| A. | -60 | B. | 70 | C. | -10 | D. | 10 |
分析 根据题意,求出(x2+$\frac{2}{x}$)5的展开式中含x4项的系数与含x7项的系数,再求(1-$\frac{3}{{x}^{3}}$)(x2+$\frac{2}{x}$)5的展开式中含x4项的系数.
解答 解:∵(x2+$\frac{2}{x}$)5的展开式中通项公式为
Tr+1=${C}_{5}^{r}$•x2(5-r)•${(\frac{2}{x})}^{r}$=2r•${C}_{5}^{r}$•x10-3r,
令10-3r=4,解得r=2,
∴该二项展开式中含x4项的系数为22•${C}_{5}^{2}$=40;
令10-3r=7,解得r=1,
∴该二项式展开式中含x7项的系数为2•${C}_{5}^{1}$=10;
∴(1-$\frac{3}{{x}^{3}}$)(x2+$\frac{2}{x}$)5的展开式中含x4项的系数为1×40-3×10=10.
故选:D.
点评 本题考查了二项式定理的应用问题,利用二项展开式的通项公式求展开式中某项的系数,是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.某几何体的三视图如图所示,则该几何体的体积是( )
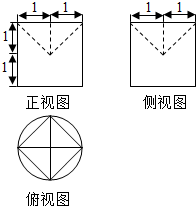

| A. | 2π-$\frac{2}{3}$ | B. | 2π-$\frac{4}{3}$ | C. | $\frac{5π}{3}$ | D. | 2π-2 |