题目内容
已知过点(0,2)的直线与抛物线y2=4x交于不同的两点A(x1,y1),B(x2,y2),计算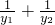 的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:________
的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:________
(根据回答的层次给分)
根据回答的层次给分
过(0,2)的直线与抛物线y2=4x交与不同的两点A(x1,y1),B(x2,y2),则 ;
;
过(0,2)的直线与抛物线y2=2px(p>0)交与不同的两点A(x1,y1),B(x2,y2),则 ;
;
过(0,b)(b≠0)的直线与抛物线y2=mx(m≠0)交与不同的两点A(x1,y1),B(x2,y2),则 .
.
分析:过(0,2)的直线与抛物线y2=4x交于不同的两点A(x1,y1),B(x2,y2),可令直线方程为y=kx+2,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系易得 ;然后根据归纳推理的办法,由此推断出过(0,2)的直线与抛物线y2=2px(p>0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质,及过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质.
;然后根据归纳推理的办法,由此推断出过(0,2)的直线与抛物线y2=2px(p>0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质,及过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质.
解答:若过(0,2)的直线斜率不存在或k=0,则直线与抛物线只有一个交点不满足要求;
若过(0,2)的直线斜率存在且不为0,则可设y=kx+2
又因为A,B两点是直线与抛物线y2=4x的交点,则

即
∴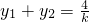 ,且
,且 
∴
因为A,B两点是直线与抛物线y2=2px(p>0)的交点,则

即
∴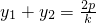 ,且
,且 
∴ .
.
由此归纳推断:过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2),则 .
.
故答案为:过(0,2)的直线与抛物线y2=4x交与不同的两点A(x1,y1),B(x2,y2),则 (1分)
(1分)
过(0,2)的直线与抛物线y2=2px(p>0)交与不同的两点A(x1,y1),B(x2,y2),则 (1分)
(1分)
过(0,b)(b≠0)的直线与抛物线y2=mx(m≠0)交与不同的两点A(x1,y1),B(x2,y2),则 (1分)
(1分)
点评:本题主要考查了抛物线的简单性质、归纳推理.归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).
过(0,2)的直线与抛物线y2=4x交与不同的两点A(x1,y1),B(x2,y2),则
 ;
;过(0,2)的直线与抛物线y2=2px(p>0)交与不同的两点A(x1,y1),B(x2,y2),则
 ;
;过(0,b)(b≠0)的直线与抛物线y2=mx(m≠0)交与不同的两点A(x1,y1),B(x2,y2),则
 .
.分析:过(0,2)的直线与抛物线y2=4x交于不同的两点A(x1,y1),B(x2,y2),可令直线方程为y=kx+2,将直线的方程代入抛物线的方程,消去y得到关于x的一元二次方程,再结合根系数的关系易得
 ;然后根据归纳推理的办法,由此推断出过(0,2)的直线与抛物线y2=2px(p>0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质,及过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质.
;然后根据归纳推理的办法,由此推断出过(0,2)的直线与抛物线y2=2px(p>0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质,及过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2)时,满足的性质.解答:若过(0,2)的直线斜率不存在或k=0,则直线与抛物线只有一个交点不满足要求;
若过(0,2)的直线斜率存在且不为0,则可设y=kx+2
又因为A,B两点是直线与抛物线y2=4x的交点,则

即

∴
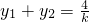 ,且
,且 
∴

因为A,B两点是直线与抛物线y2=2px(p>0)的交点,则

即

∴
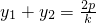 ,且
,且 
∴
 .
.由此归纳推断:过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2),则
 .
.故答案为:过(0,2)的直线与抛物线y2=4x交与不同的两点A(x1,y1),B(x2,y2),则
 (1分)
(1分)过(0,2)的直线与抛物线y2=2px(p>0)交与不同的两点A(x1,y1),B(x2,y2),则
 (1分)
(1分)过(0,b)(b≠0)的直线与抛物线y2=mx(m≠0)交与不同的两点A(x1,y1),B(x2,y2),则
 (1分)
(1分)点评:本题主要考查了抛物线的简单性质、归纳推理.归纳推理的一般步骤是:(1)通过观察个别情况发现某些相同性质;(2)从已知的相同性质中推出一个明确表达的一般性命题(猜想).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
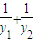 的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:
的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例: