题目内容
已知过点(0,2)的直线与抛物线y2=4x交于不同的两点A(x1,y1),B(x2,y2),计算
+
的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:______
(根据回答的层次给分)
| 1 |
| y1 |
| 1 |
| y2 |
(根据回答的层次给分)
若过(0,2)的直线斜率不存在或k=0,则直线与抛物线只有一个交点不满足要求;
若过(0,2)的直线斜率存在且不为0,则可设y=kx+2
又因为A,B两点是直线与抛物线y2=4x的交点,则
即 y2-
y+
=0
∴y1+y2=
,且 y1•y2=
∴
+
=
因为A,B两点是直线与抛物线y2=2px(p>0)的交点,则
即 y2-
y+
=0
∴y1+y2=
,且 y1•y2=
∴
+
=
.
由此归纳推断:过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2),则
+
=
.
故答案为:过(0,2)的直线与抛物线y2=4x交与不同的两点A(x1,y1),B(x2,y2),则
+
=
(1分)
过(0,2)的直线与抛物线y2=2px(p>0)交与不同的两点A(x1,y1),B(x2,y2),则
+
=
(1分)
过(0,b)(b≠0)的直线与抛物线y2=mx(m≠0)交与不同的两点A(x1,y1),B(x2,y2),则
+
=
(1分)
若过(0,2)的直线斜率存在且不为0,则可设y=kx+2
又因为A,B两点是直线与抛物线y2=4x的交点,则
|
即 y2-
| 4 |
| k |
| 8 |
| k |
∴y1+y2=
| 4 |
| k |
| 8 |
| k |
∴
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| 2 |
因为A,B两点是直线与抛物线y2=2px(p>0)的交点,则
|
即 y2-
| 2p |
| k |
| 4p |
| k |
∴y1+y2=
| 2p |
| k |
| 4P |
| k |
∴
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| 2 |
由此归纳推断:过(0,b)的直线与抛物线y2=mx(m≠0)交于不同的两点A(x1,y1),B(x2,y2),则
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| b |
故答案为:过(0,2)的直线与抛物线y2=4x交与不同的两点A(x1,y1),B(x2,y2),则
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| 2 |
过(0,2)的直线与抛物线y2=2px(p>0)交与不同的两点A(x1,y1),B(x2,y2),则
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| 2 |
过(0,b)(b≠0)的直线与抛物线y2=mx(m≠0)交与不同的两点A(x1,y1),B(x2,y2),则
| 1 |
| y1 |
| 1 |
| y2 |
| 1 |
| b |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
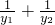 的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:________
的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:________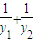 的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例:
的值,由此归纳一条与抛物线有关的性质,使得上述计算结果是性质的一个特例: