题目内容

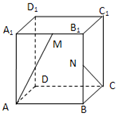
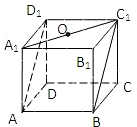
在正方体ABCD-A1B1C1D1中，BC1与平面BDD1B1所成的角为（　　）
A．30°B．45°C．60°D．90°
连接A1C1，交B1D1于O，连接BO，
得到∠OBC1是BC1与平面BDD1B1所成的角，
设正方体的棱长为2，
在直角三角形OBC1中，由题意，得
OC1=
2
，BC1=2
2
，
∴sin∠OBC1=
2
2
2
=
1
2
，∴∠OBC1中=30°
故直线DE与平面ABCD所成角的大小是：30°．
故选A．
练习册系列答案
相关题目
在正方体ABCD-A1B1C1D1中，M、N分别为棱A1B1和BB1的中点，那么异面直线AM和CN所成角的余弦值是（　　）
A．
3
2
B．
10
2
C．
2
5
D．-
2
5
已知四面体ABCD的六条棱长都是1，则直线AD与平面ABC的夹角的余弦值为______．
在三棱柱ABC-A1B1C1中，CC1⊥平面ABC，∠ACB=90°，AB=2，BC=1，AA1=
3
．
（1）求证：A1C⊥平面AB1C1；
（2）求A1B1与平面AB1C1所成的角的正弦值．
如图，三棱锥P-ABC中，∠ACB=90°，PA⊥底面ABC．
（I）求证：平面PAC⊥平面PBC；
（II）若AC=BC=PA，M是PB的中点，求AM与平面PBC所成角的正切值．
如图，圆锥顶点为P，底面圆心为O，其母线与底面所成的角为22.5°，AB和CD是底面圆O上的两条平行的弦，轴OP与平面PCD所成的角为60°，
（1）证明：平面PAB与平面PCD的交线平行于底面；
（2）求cos∠COD．
如图，正方体ABCD-A1B1C1D1直线AD1与平面A1C1的夹角为（　　）
A．30°B．45°C．90°D．60°
如图，S是正方形ABCD所在平面外一点，且SD⊥面ABCD，AB=1，SB=
3
．
（1）求证：BC⊥SC；
（2）设M为棱SA中点，求异面直线DM与SB所成角的大小
（3）求面ASD与面BSC所成二面角的大小．
把边长为a的正△ABC沿高线AD折成60°的二面角，这时A到边BC的距离是（　　）
A．
15
4
a		B．
6
3
a		C．
13
4
a		D．
3
2
a

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网