题目内容
已知正三棱柱ABC—A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是边AC,A1C1的中点,建立如图所示的空间直角坐标系.
⑴求正三棱柱的侧棱长.
⑵若M为BC1的中点,试用基向量 、
、 、
、 表示向量
表示向量 ;
;
⑶求异面直线AB1与BC所成角的余弦值.

【答案】
(1)由已知B( ,0,0)
A(0,-1,0)
,0,0)
A(0,-1,0)  (
( ,0,m)
,0,m)
C(0,1,0),  (0,1,
m)
(0,1,
m)
∴ 1=(
1=( ,1,m)
,1,m)
 =(-
=(- ,1,m)
,1,m)
又有 1⊥
1⊥ ∴
∴ 1.
1. =0=-3+1+
=0=-3+1+
∴ =2 ∴m=
=2 ∴m=

(2)  =(
=( +
+ +
+ )
)
(3)由(1)知 1=(
1=( ,1,
,1,
 )
)
Cos< 1,BC>=-
1,BC>=-
∴异面直线AB1与BC所成角的余弦值为
【解析】略

练习册系列答案
相关题目
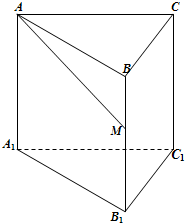 如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ.
如图,已知正三棱柱ABC-A1B1C1的底面边长为1,高为h(h>2),动点M在侧棱BB1上移动.设AM与侧面BB1C1C所成的角为θ. 已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.
已知正三棱柱ABC-A1B1C1的每条棱长均为a,M为棱A1C1上的动点.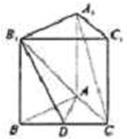 如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1.
如图,已知正三棱柱ABC-A1B1C1中,D是BC的中点,AA1=AB=1. (2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.
(2009•湖北模拟)如图,已知正三棱柱ABC-A1B1C1各棱长都为a,P为棱A1B上的动点.