题目内容
6.已知集合A={x|x2-2px+p2+2p+2=0,x∈R},且A∩R+=∅,求实数p的取值范围.分析 化简可得(x-p)2=-2p-2,从而讨论确定方程的解的个数,从而解集合A,再解得.
解答 解:∵x2-2px+p2+2p+2=0,
∴(x-p)2=-2p-2,
①当-2p-2<0,即p>-1时,
A=∅,故A∩R+=∅;
②当-2p-2=0,即p=-1时,
A={-1},故A∩R+=∅;
③当p<-1时,
p+$\sqrt{-2p-2}$≤0,
解之可得恒成立;
综上所述,实数p的取值范围为R.
点评 本题考查了集合的化简与分类讨论的思想应用,同时考查了集合的运算.

练习册系列答案
相关题目
6.若实数a,b在区间[0,$\sqrt{2}$]上取值,则函数f(x)=$\frac{2}{3}$ax3+bx2+ax在R上有两个相异极值点的概率是( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | $\frac{\sqrt{2}}{8}$ | D. | $\frac{1}{2}$ |
3.用数学归纳法证明不等式$\frac{n+2}{2}$<1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+…+$\frac{1}{{2}^{n}}$<n+1(n>1,n∈N*)的过程中,当n=2时,中间式子为( )
| A. | 1 | B. | 1+$\frac{1}{2}$ | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$ | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ |
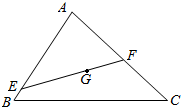 如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.
如图,G是△ABC的重心,过G的直线与边AB,AC分别相交于点E,F,若AE=mAB,AF=nAC(mn≠0),求$\frac{1}{m}$+$\frac{1}{n}$的值.