题目内容
经过点(0,-1)作圆C:x2+y2-6x+7=0的切线,切点分别为A和B,点Q是圆C上一点,则△ABQ面积的最大值为________.

分析:先确定直线AB的方程,利用点到直线的距离公式,求出|AB|,△ABQ面积的最大值时,Q到AB的距离最大,此时CQ⊥AB
,确定Q到AB的最大距离,即可得到结论.
解答:圆C:x2+y2-6x+7=0化为标准方程为(x-3)2+y2=2,
以(0,-1)与C连线为直径的圆的方程为x2+y2-3x+y=0,两圆方程相减,可得直线AB的方程为3x+y-7=0
圆心C到直线AB的距离为
 =
=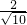 ,∴|AB|=2
,∴|AB|=2 =
=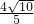
△ABQ面积的最大值时,Q到AB的距离最大,此时CQ⊥AB
∵点(0,-1)到直线AB的距离为
 =
= ,点(0,-1)与圆心的距离为
,点(0,-1)与圆心的距离为
∴Q到AB的距离最大值为
 +
+ -
- =
=
∴△ABQ面积的最大值为
 =
=
故答案为

点评:本题考查直线与圆的位置关系,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
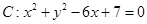 的切线,切点分别为A和B,点Q是圆C上一点,则
的切线,切点分别为A和B,点Q是圆C上一点,则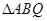 面积的最大值为 。
面积的最大值为 。