题目内容
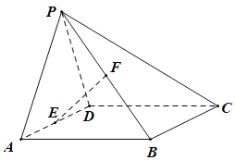
【题目】如图,在四棱锥![]() 中,
中,![]() 是边长为4的正三角形,
是边长为4的正三角形,![]() 且
且![]() ,
,![]() ,
,![]() ,
,![]() ,M为AB中点.
,M为AB中点.
(Ⅰ)证明:![]() 平面ADE;
平面ADE;
(Ⅱ)求直线CA与平面BCDE所成角的正弦值.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)取AE的中点F,连接MF、FD,只需证明四边形MFDC为平行四边形,因为点M为AB的中点,所以![]() ,且
,且![]() ,则易证.
,则易证.
(Ⅱ)先证明![]() 平面ADE,作
平面ADE,作![]() 于
于![]() ,再证明
,再证明![]() 平面CDEB,所以
平面CDEB,所以![]() 为直线CA与平面BCDE所成的角,利用
为直线CA与平面BCDE所成的角,利用![]() ,求出
,求出![]() ,则直线CA与平面BCDE所成角的正弦值可求.
,则直线CA与平面BCDE所成角的正弦值可求.
(Ⅰ)证明:
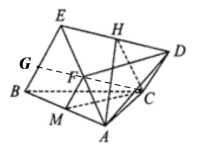
取AE的中点F,连接MF,FD,
因为点M为AB的中点,
所以![]() ,且
,且![]() ,
,
又因为![]() 且
且![]() ,
,
所以![]() ,
,![]() ,
,
所以四边形MFDC为平行四边形,所以![]() ,
,
又因为![]() 平面ADE,
平面ADE,![]() 平面ADE,
平面ADE,
所以![]() 平面ADE.
平面ADE.
(Ⅱ)解:因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]() ,
,
又![]() ,
,![]() ,
,
所以![]() 平面ADE,
平面ADE,
又![]() 平面CDEB,
平面CDEB,
所以平面![]() 平面CDEB,
平面CDEB,
作![]() 于
于![]() ,因为平面
,因为平面![]() 平面
平面![]() ,
,
所以![]() 平面CDEB,连接CH,
平面CDEB,连接CH,
所以![]() 为直线CA与平面BCDE所成的角.
为直线CA与平面BCDE所成的角.
因为![]() 平面ADE,所以
平面ADE,所以![]() ,
,
在直角梯形BCDE中,作![]() 于
于![]() ,则四边形
,则四边形![]() 为矩形,
为矩形,![]()
则![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,
在直角三角形ACD中,![]() ,
,
又![]() ,
,
在![]() 中,
中,![]()
所以![]()
所以![]() ,
,
所以![]() ,
,
所以直线CA与平面BCDE所成角的正弦值为![]() .
.

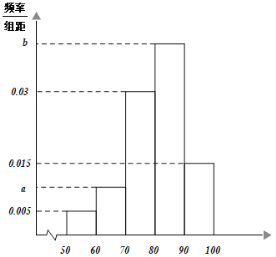
【题目】某公司A产品生产的投入成本x(单位:万元)与产品销售收入y(单位:十万元)存在较好的线性关系,下表记录了该公司最近8次该产品的相关数据,且根据这8组数据计算得到y关于x的线性回归方程为![]() .
.
x(万元) | 6 | 7 | 8 | 11 | 12 | 14 | 17 | 21 |
y(十万元) | 1.2 | 1.5 | 1.7 | 2 | 2.2 | 2.4 | 2.6 | 2.9 |
(1)求![]() 的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
的值(结果精确到0.0001),并估计公司A产品投入成本30万元后产品的销售收入(单位:十万元).
(2)该公司B产品生产的投入成本u(单位:万元)与产品销售收入v(单位:十万元)也存在较好的线性关系,且v关于u的线性回归方程为![]() .
.
(i)估计该公司B产品投入成本30万元后的毛利率(毛利率![]() );
);
(ii)判断该公司A,B两个产品都投入成本30万元后,哪个产品的毛利率更大.