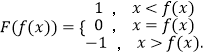Question

【题目】设点O是平行四边形ABCD两条对角线的交点，给出下列向量组：
① 与 ；
② 与 ；
③ 与 ；
④ 与 ．
其中可作为该平面其他向量基底的是（ ）
A.①②
B.①③
C.①④
D.③④

Answer 1

【答案】B
【解析】解：如下图所示：

① 与 不共线，故①可作为这个平行四边形所在平面表示它的所有向量的基底；② 与 共线，故②不可作为这个平行四边形所在平面表示它的所有向量的基底；③ 与 不共线，故③可作为这个平行四边形所在平面表示它的所有向量的基底；④ 与 共线，故④不可作为这个平行四边形所在平面表示它的所有向量的基底；

所以答案是：B．

【考点精析】本题主要考查了平面向量的基本定理及其意义的相关知识点，需要掌握如果、是同一平面内的两个不共线向量，那么对于这一平面内的任意向量，有且只有一对实数、，使才能正确解答此题．