Question

【题目】某同学用“五点法”画函数 在区间[﹣ ， ]上的图象时，列表并填入了部分数据，如表：

2x﹣	﹣ π	﹣π	﹣	0		π
x	﹣	﹣	﹣
f（x）

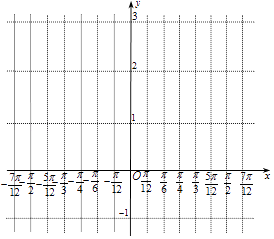
（1）请将上表数据补充完整，并在给出的直角坐标系中，画出f（x）在区间[﹣ ， ]上的图象；
（2）求f（x）的最小值及取最小值时x的集合；
（3）求f（x）在 时的值域．

Answer 1

【答案】
（1）解：数据补全如下表：

2x﹣	﹣	﹣π	﹣	0
x	﹣	﹣	﹣
f（x）		1	﹣1	1	3

故f（x）在区间[﹣ ， ]上的图象如图所示．

（2）解：当 ，

即 时，f（x）取最小值﹣1．

取最小值时x的集合为

（3）解：当 时， ，

故

所以 ，即f（x）在 时的值域为

【解析】（1）先把数据补全，利用描点法能在给出的直角坐标系中，画出f（x）在区间[﹣ ， ]上的图象．（2）利用正弦函数的图象及性质能求出函数 的最小值及取最小值时x的集合．（3）当 时， ，从而 ，由此能求出f（x）在 时的值域．
【考点精析】掌握正弦函数的单调性和五点法作函数y=Asin（ωx+φ）的图象是解答本题的根本，需要知道正弦函数的单调性：在上是增函数；在上是减函数；描点法及其特例—五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）．