题目内容
【题目】已知等比数列
的前
项和为
，且
， 
， 
．
（1）求数列
的通项公式；
（2）数列
中， 
，求数列
的前
项和
．
【答案】（1）
（2）
【解析】试题分析：（1）由题意列出关于首项和公比的方程组，即可求出公比
，写出通项公式；（2）根据通项公式的结构特点，采用错位相减法求其前n项和即可.
试题解析：
（1）由
得
，又
，∴
，
又数列
成等比数列，设公比
，则
∴
或
（
与
矛盾，舍），
∴
， 
；
（2）
，∴
，
=﹣2×2﹣2﹣1×2﹣1+0+…+（n﹣3）×2n﹣3，
2
=﹣2×2﹣1﹣1×20+0+…+（n﹣3）×2n﹣2，
相减得
=2×2﹣2﹣（2﹣1+20+…+2n﹣3）+（n﹣3）×2n﹣2=
﹣（2n﹣2﹣
）+（n﹣3）×2n﹣2
=（n﹣4）×2n﹣2+1， 
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】某同学用“五点法”画函数 
在区间[﹣ 
， ]上的图象时，列表并填入了部分数据，如表：
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f（x） |
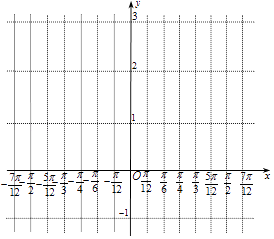
（1）请将上表数据补充完整，并在给出的直角坐标系中，画出f（x）在区间[﹣ ， ]上的图象；
（2）求f（x）的最小值及取最小值时x的集合；
（3）求f（x）在 
时的值域．
