题目内容
【题目】设f(x)=asin 2x+bcos 2x,其中a,b∈R,ab≠0.若f(x)≤|f( ![]() )|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ①
)|对一切x∈R恒成立,则以下结论正确的是(写出所有正确结论的编号). ① ![]() ;②
;② ![]() ≥
≥ ![]() ;
;
③f(x)的单调递增区间是(kπ+ ![]() ,kπ+
,kπ+ ![]() )(k∈Z);
)(k∈Z);
④f(x)既不是奇函数也不是偶函数.
【答案】①②④
【解析】解:由f(x)=asin 2x+bcos 2x= ![]() sin(2x+φ). ∵f(x)≤|f(
sin(2x+φ). ∵f(x)≤|f( ![]() )|对一切x∈R恒成立
)|对一切x∈R恒成立
∴当x= ![]() 时,函数取得最大值,即2×
时,函数取得最大值,即2× ![]() +φ=
+φ= ![]() ,解得:φ=
,解得:φ= ![]() .
.
故得f(x)= ![]() sin(2x+
sin(2x+ ![]() ).
).
则f( ![]() )=
)= ![]() sin(2×
sin(2× ![]() +
+ ![]() )=0,∴①对.
)=0,∴①对.
②f( ![]() )=
)= ![]() sin(2×
sin(2× ![]() +
+ ![]() )=-
)=- ![]()
f( ![]() )=
)= ![]() sin(2×
sin(2× ![]() +
+ ![]() )=
)= ![]() ,∴
,∴ ![]() ≥
≥ ![]() ,∴②对.
,∴②对.
由 ![]() 2x+
2x+ ![]() ,(k∈Z)
,(k∈Z)
解得:- ![]() +kπ≤x≤
+kπ≤x≤ ![]() +kπ,(k∈Z)
+kπ,(k∈Z)
∴f(x)的单调递增区间是(kπ- ![]() ,kπ+
,kπ+ ![]() )(k∈Z);∴③不对
)(k∈Z);∴③不对
f(x)的对称轴2x+ ![]() =
= ![]() +kπ,(k∈Z);∴③
+kπ,(k∈Z);∴③
解得:x= ![]() kπ+
kπ+ ![]() ,不是偶函数,
,不是偶函数,
当x=0时,f(0)= ![]() ,不关于(0,0)对称,
,不关于(0,0)对称,
∴f(x)既不是奇函数也不是偶函数.
所以答案是①②④.

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数 ![]() 在区间[﹣
在区间[﹣ ![]() ,
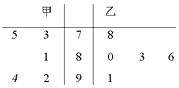
, ![]() ]上的图象时,列表并填入了部分数据,如表:
]上的图象时,列表并填入了部分数据,如表:
2x﹣ | ﹣ | ﹣π | ﹣ | 0 |
|
|
x | ﹣ | ﹣ | ﹣ |
|
|
|
f(x) |
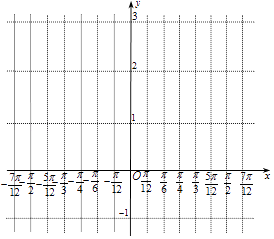
(1)请将上表数据补充完整,并在给出的直角坐标系中,画出f(x)在区间[﹣ ![]() ,
, ![]() ]上的图象;
]上的图象;
(2)求f(x)的最小值及取最小值时x的集合;
(3)求f(x)在 ![]() 时的值域.
时的值域.