Question

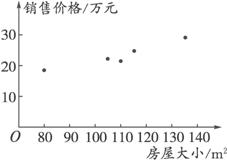
以下是收集到的新房屋的销售价格y和房屋的大小x的数据.

房屋大小/m2	115	110	80	135	105
销售价格/万元	24.8	21.6	18.4	29.2	22

(1)画出数据的散点图;

(2)求线性回归方程及相关系数r,并作出评价.

Answer 1

解:(1)

(2)

i	xi	yi	xi2	yi2	xiyi
1	115	24.8	13 225	615.04	2 852
2	110	21.6	12 100	466.56	2 376
3	80	18.4	6 400	338.56	1 472
4	135	29.2	18 225	852.64	3 942
5	105	22	11 025	484	2 310
∑	545	116	60 975	2 756.8	12 952

==109,==23.2,

b=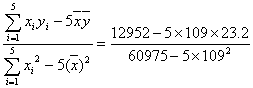==0.196,

a=-b=23.2-0.196×109=1.836,

∴回归方程为y=1.836+0.196x,

r==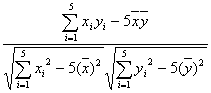

==0.96,拟合程度较高.