题目内容
已知
1、
2、
3为不共面向量,若
=
1+
2+
3,
=
1-
2+
3,
=
1+
2-
3,
=
1+2
2+3
3,且
=x
+y
+z
,则x、y、z分别为
,-
,-1
,-
,-1.
| e |
| e |
| e |
| a |
| e |
| e |
| e |
| b |
| e |
| e |
| e |
| c |
| e |
| e |
| e |
| d |
| e |
| e |
| e |
| d |
| a |
| b |
| c |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
分析:由
=x
+y
+z
,得
+2
+3
=x(
+
+
)+y(
-
+
)+z(
+
-
)整理为
+2
+3
=(x+y+z)
+(x-y+z)
+(x+y-z)
,利用向量相等即可得出.
| d |
| a |
| b |
| c |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
解答:解:由
=x
+y
+z
,得
+2
+3
=x(
+
+
)+y(
-
+
)+z(
+
-
)
化为
+2
+3
=(x+y+z)
+(x-y+z)
+(x+y-z)
,
由向量相等条件可得
,解得
,
故答案为
,-
,-1.
| d |
| a |
| b |
| c |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
化为
| e1 |
| e2 |
| e3 |
| e1 |
| e2 |
| e3 |
由向量相等条件可得
|
|
故答案为
| 5 |
| 2 |
| 1 |
| 2 |
点评:熟练掌握向量的运算法则和向量相等是解题的关键.

练习册系列答案
相关题目
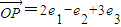 ,
,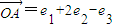 ,
,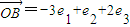 ,
,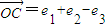 .
.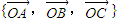 作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量
作为空间的一个基底?若不能,说明理由;若能,试以这一基底表示向量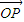 .
.