题目内容
已知{
，
，
}是空间的一个基底，下列四组向量中，能作为空间一个基底的是（ ）
①
，2
，
-
②2
，
-
，
+2
③2
+
，
+
，-
+5
④
，
+
，
+
．
| e1 |
| e2 |
| e3 |
①
| e1 |
| e2 |
| e2 |
| e3 |
②2
| e2 |
| e2 |
| e1 |
| e2 |
| e1 |
③2
| e1 |
| e2 |
| e2 |
| e3 |
| e1 |
| e3 |
④
| e3 |
| e1 |
| e3 |
| e1 |
| e3 |
| A、①② | B、②④ | C、③④ | D、①③ |
分析：利用平面向量基本定理、空间向量基底的意义即可判断出．
解答：解：①假设存在非0实数a，b，c使得a
+b•2
+c(
-
)=
，化为a
+(2b+c)
-c
=
，
∵{
，
，
}是空间的一个基底，
∴
，解得a=b=c=0，
故假设不成立，因此
，2
，
-
可以作为空间的一个基底．
②∵2
，
-
，
+2
一定是共面向量，因此不能作为空间向量的一个基底；
③假设存在实数a，b，c使得a(2
+
)+b(
+
)+c(-
+5
)=
，化为，(2a-c)
+(a+b)
+(b+5c)
=
，
∵{
，
，
}是空间的一个基底，
∴
，解得a=b=c=0，故假设不成立．
因此可以作为空间的一个基底．
④
，
+
，
+
一定是共面向量，因此不能作为空间向量的一个基底．
综上可知：只有①③能作为空间一个基底．
故选：D．
| e1 |
| e2 |
| e2 |
| e3 |
| 0 |
| e1 |
| e2 |
| e3 |
| 0 |
∵{
| e1 |
| e2 |
| e3 |
∴
|
故假设不成立，因此
| e1 |
| e2 |
| e2 |
| e3 |
②∵2
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
③假设存在实数a，b，c使得a(2
| e1 |
| e2 |
| e2 |
| e3 |
| e1 |
| e3 |
| 0 |
| e1 |
| e2 |
| e3 |
| 0 |
∵{
| e1 |
| e2 |
| e3 |
∴
|
因此可以作为空间的一个基底．
④
| e3 |
| e1 |
| e3 |
| e1 |
| e3 |
综上可知：只有①③能作为空间一个基底．
故选：D．
点评：本题考查了平面向量基本定理、空间向量基底的意义，属于基础题．
练习册系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
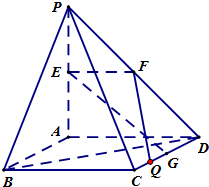（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（2013•浦东新区二模）（1）设椭圆C1：