题目内容
已知{e1，e2，e3}为空间的一个基底，且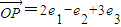
，
，
，
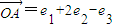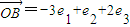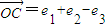．（1）判断P，A，B，C四点是否共面；
（2）能否以
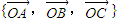作为空间的一个基底？若不能，说明理由；若能，试以这一基底表示向量
．
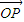【答案】分析：（1）假设假设四点共面，则存在实数x，y，z使
，且x+y+z=1，
把各向量的坐标代入，解出的x、y、z值看是否满足x+y+z=1．
（2）任何三个不共面的向量构成空间向量的一个基底，用反证法证明向量
，
，
共面不可能，
因此
可以作为空间的一个基底，待定系数法求
．
解答：解：（1）假设四点共面，则存在实数x，y，z使
，
且x+y+z=1，
即2e1-e2+3e3=x（e1+2e2-e3）+y（-3e1+e2+2e3）+z（e1+e2-e3）．（4分）
比较对应的系数，得一关于x，y，z的方程组
解得
与x+y+z=1矛盾，故四点不共面；（6分）
（2）若向量
，
，
共面，则存在实数m，n使
，
同（1）可证，这不可能，
因此
可以作为空间的一个基底，
令
，
，
，
由e1+2e2-e3=a，-3e1+e2+2e3=b，e1+e2-e3=c联立得到方程组，
从中解得
（10分）
所以
．（12分）
点评：本题考查向量共面的条件，使用了反证法，及用待定系数法表示空间向量．
，且x+y+z=1，把各向量的坐标代入，解出的x、y、z值看是否满足x+y+z=1．
（2）任何三个不共面的向量构成空间向量的一个基底，用反证法证明向量
，，共面不可能，因此
可以作为空间的一个基底，待定系数法求．解答：解：（1）假设四点共面，则存在实数x，y，z使
，且x+y+z=1，
即2e1-e2+3e3=x（e1+2e2-e3）+y（-3e1+e2+2e3）+z（e1+e2-e3）．（4分）
比较对应的系数，得一关于x，y，z的方程组
解得
与x+y+z=1矛盾，故四点不共面；（6分）
（2）若向量
，，共面，则存在实数m，n使，同（1）可证，这不可能，
因此
可以作为空间的一个基底，令
，，，由e1+2e2-e3=a，-3e1+e2+2e3=b，e1+e2-e3=c联立得到方程组，
从中解得
（10分）所以
．（12分）点评：本题考查向量共面的条件，使用了反证法，及用待定系数法表示空间向量．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
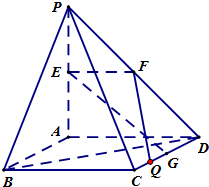（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（2013•浦东新区二模）（1）设椭圆C1：