题目内容
已知函数![]() ,存在实数
,存在实数![]() 、
、![]() 满足下列条件:①
满足下列条件:①![]() ;②
;②![]() ;③
;③![]() .
. ![]()
(Ⅰ) 证明: ![]() ;
;
(Ⅱ)求![]() 的取值范围;
的取值范围;
(III)若函数![]() ,证明:当
,证明:当![]() 时,
时,![]() .
.
解析:(1)![]() 所以
所以![]() ,由
,由![]() ,得
,得![]() ,
,
由![]() 知
知![]() .
.
故![]() 和
和![]() 是方程
是方程![]() 的两个实根, ∴方程有解, ∴D=4-
的两个实根, ∴方程有解, ∴D=4-![]() ³0,得
³0,得![]() . 4分
. 4分
(2)由![]() 得
得![]() +
+![]() =4, 从而
=4, 从而![]() , 所以
, 所以![]() ,由b¢=0得
,由b¢=0得![]() 或
或![]() .又
.又![]() , ∴当
, ∴当![]() 变化时,b¢,b的变化情况如下表:
变化时,b¢,b的变化情况如下表:
| 0 | (0,2) | 2 | (2,3) | 3 |
b¢ |
| + | 0 | - |
|
b | 0 | | 极大值12 | ¯ | 0 |
∴0£b£12 4分
(3)因为![]() , 所以
, 所以![]()
又![]() 所以
所以

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 存在单调递减区间,则实数
存在单调递减区间,则实数 的取值
的取值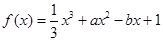 (
(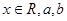 为实数)有极值,且在
为实数)有极值,且在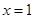 处的切线与直线
处的切线与直线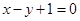 平行.
平行.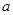 的取值范围;
的取值范围;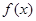 的极小值为
的极小值为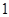 ,若存在,求出实数
,若存在,求出实数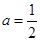 ,
,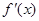 ,令
,令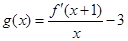
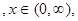
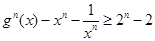
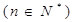
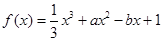 (
( 为实数)有极值,且在
为实数)有极值,且在 处的切线与直线
处的切线与直线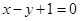 平行.
平行. 的取值范围;
的取值范围; 的极小值为1,若存在,求出实数
的极小值为1,若存在,求出实数 ,
, ,令
,令



 存在单调递减区间,则实数a的取值范围为 .
存在单调递减区间,则实数a的取值范围为 .