Question

如图，设点A和B是抛物线y²=4px上原点以外的两个动点，已知OA⊥OB，OM⊥AB，求动点M的轨迹方程，并说明它表示什么曲线.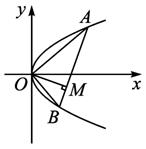

Answer 1

解：点A、B在抛物线y²=4px上，设A(,y_A),B(,y_B),则

=(,y_A),=(,y_B), =(,y_B-y_A).

    因为⊥，所以·+y_A·y_B=0，即y_A·y_B=-16p².

    设M=(x,y)，则=(x,y), =(-x,y_A-y), =(-x,y_B-y).

    因为⊥，所以x·+y(y_B-y_A)=0,即x·+y=0.

    又因为A、B、M三点共线，所以∥,

    即(-x)(y_B-y)=(-x)(y_A-y).

    化简得y_A+y_B=,

    所以x·+y=0，

    即x²+y²-4px=0.

    因为A、B是原点以外的两点，所以x≠0.所以点M的轨迹是以(2p,0)为圆心，以2p为半径的圆(去掉原点).