题目内容

双曲线x2-y2=a2的两个焦点分别为F1、F2，P为双曲线上的任意一点，求证：|PF1|、|PO|、|PF2|成等比数列.

证明：设P点的坐标为（x,y），则|PO|2=x2+y2.

?∵双?曲线的离心率e=，准线方程是x=±，

∴,，

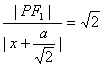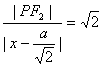∴|PF1|=|x+a|,|PF2|=|x-a|，

∴|PF1|·|PF2|=|2x2-a2|=|x2+y2|=|PO|2，

即|PF1|、|PO|、|PF2|成等比数列.

练习册系列答案
相关题目
F1、F2分别是双曲线x2-y2=1的两个焦点，O为坐标原点，圆O是以F1F2为直径的圆，直线l：y=kx+b与圆O相切，并与双曲线交于A、B两点．向量
AB
|
AB
|
在向量
F1F2
方向的投影是p．
（1）根据条件求出b和k满足的关系式；
（2）当(
OA
•
OB
)p2=1时，求直线l的方程；
（3）当(
OA
•
OB
)p2=m，且满足2≤m≤4时，求△AOB面积的取值范围．
已知双曲线x2-y2=2的左、右焦点分别为F1，F2，过点F2的动直线与双曲线相交于A，B两点．若动点M满足
F1M
=
F1A
+
F1B
+
F1O
（其中O为坐标原点），求点M的轨迹方程；
双曲线x2-y2=1左支上一点（a，b）到其渐近线y=x的距离是
2
，则a+b的值为
 
．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，双曲线x2-y2=1的渐近线与椭圆有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆C的方程为
x2
20
+
y2
5
=1
x2
20
+
y2
5
=1
．
（2012•山东）已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
3
2
，与双曲线x2-y2=1的渐近线有四个交点，以这四个交点为顶点的四边形的面积为16，则椭圆c的方程为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网