题目内容
在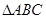 中,角
中,角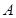 、
、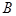 、
、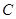 的对边分别为
的对边分别为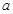 、
、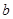 、
、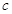 .设向量
.设向量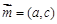 ,
,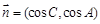 .
.
(1)若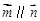 ,
,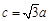 ,求角
,求角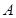 ;(2)若
;(2)若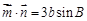 ,
,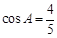 ,求
,求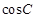 的值.
的值.
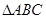 中,角
中,角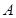 、
、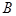 、
、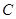 的对边分别为
的对边分别为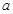 、
、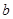 、
、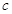 .设向量
.设向量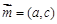 ,
,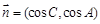 .
.(1)若
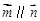 ,
,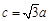 ,求角
,求角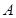 ;(2)若
;(2)若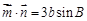 ,
,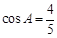 ,求
,求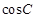 的值.
的值.(1) (2)
(2)
 (2)
(2)
试题分析:(1)解三角形,一般利用正余弦定理,将等量关系统一成角或边.首先由向量平行坐标关系得
 再根据正弦定理或余弦定理,将等式化为
再根据正弦定理或余弦定理,将等式化为 或
或 ,结合三角形中角的限制条件,得
,结合三角形中角的限制条件,得 或
或 ,或利用因式分解化为
,或利用因式分解化为 ,从而有
,从而有 ,(2)由向量数量积坐标关系得
,(2)由向量数量积坐标关系得 再根据正弦定理或余弦定理,将等式化为
再根据正弦定理或余弦定理,将等式化为 或
或 ,再由两角和余弦公式求出
,再由两角和余弦公式求出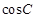 的值.
的值.试题解析:(1)∵
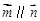 ,∴
,∴ .由正弦定理,得
.由正弦定理,得 .
.化简,得
 .… 2分∵
.… 2分∵ ,∴
,∴ 或
或 ,从而
,从而 (舍)或
(舍)或 .∴
.∴ .… 4分 在Rt△ABC中,
.… 4分 在Rt△ABC中, ,
, .…6分
.…6分(2)∵
 ,∴
,∴ .
.由正弦定理,得
 ,从而
,从而 .
.∵
 ,∴
,∴ . 从而
. 从而 . 8分
. 8分∵
 ,
, ,∴
,∴ ,
, . 10分
. 10分∵
 ,∴
,∴ ,从而
,从而 ,B为锐角,
,B为锐角, . 12分
. 12分∴
 =
= . 14分
. 14分
练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 中,角
中,角 、
、 、
、 对的边分别为
对的边分别为 、
、 、
、 ,且
,且
 的值;
的值; ,求
,求 .
. acos C.
acos C.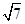 ,且
,且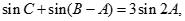 求△ABC的面积.
求△ABC的面积. 中,
中, 分别是
分别是 的对边长,已知
的对边长,已知 ,求
,求 的大小及
的大小及 的值.
的值.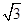 a,则( )
a,则( ) bc,sin C=2
bc,sin C=2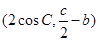 ,e2=
,e2=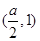 ,且e1⊥e2.
,且e1⊥e2. 的内角
的内角 所对边的长分别为
所对边的长分别为 ,若
,若 ,则角
,则角 = ( )
= ( )



 中,
中, ,则
,则 _____________.
_____________.