题目内容
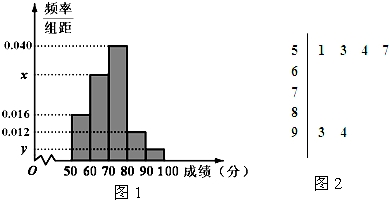
5. 某学校计划举办“国学”系列讲座,为了解学生的国学素养,在某班随机地抽取8名同学进行国学素养测试,这8名同学的测试成绩的茎叶图如图所示.
某学校计划举办“国学”系列讲座,为了解学生的国学素养,在某班随机地抽取8名同学进行国学素养测试,这8名同学的测试成绩的茎叶图如图所示.(Ⅰ)根据这8名同学的测试成绩,估计该班学生国学素养测试的平均成绩;
(Ⅱ)规定成绩大于75分为优秀,若从这8名同学中随机选取一男一女两名同学,求这两名同学的国学素养测试成绩均为优秀的概率.
分析 (Ⅰ)利用茎叶图及平均数定义能出这8名同学的平均成绩.
(Ⅱ)设“两名同学的国学素养测试成绩均为优秀”为事件A,由题意得从8名学生中随机选取一男一女两名同学国学素养测试成绩,利用列举法求出所有可能的结果有16个,事件A包含的结果有3个,由此能求出这两名同学的国学素养测试成绩均为优秀的概率.
解答 解:(Ⅰ)设这8名同学的平均成绩为$\overline{x}$,
则$\overline{x}$=$\frac{1}{8}$(64+72+74+78+56+77+78+85)=73.
(Ⅱ)设“两名同学的国学素养测试成绩均为优秀”为事件A,
由题意得从8名学生中随机选取一男一女两名同学国学素养测试成绩,
所有可能的结果有16个,分别为:
(64,56),(64,77),(64,78),(64,85),(72,56),(72,77),(72,78),(72,85),
(74,56),(74,77),(74,78),(74,85),(78,56),(78,77),(78,78),(78,85),
事件A包含的结果有3个,分别为:(78,77),(78,78),(78,85),
∴这两名同学的国学素养测试成绩均为优秀的概率P(A)=$\frac{3}{16}$.
点评 本题考查平均数、概率的求法,考查茎叶图、平均数、概率、列举法等基础知识,考查运算求解能力,是基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
18.由曲线y=x2和直线y=x+2围成封闭图形的面积是( )
| A. | $\frac{10}{3}$ | B. | $\frac{7}{6}$ | C. | $\frac{9}{2}$ | D. | $\frac{13}{6}$ |
13.复数$\frac{3+4i}{i}$=( )
| A. | -4-3i | B. | -4+3i | C. | 4+3i | D. | 4-3i |
10.下列结论中正确的是( )
| A. | 若两个变量的线性相关性越强,则相关系数的绝对值越接近于0 | |
| B. | 回归直线至少经过样本数据中的一个点 | |
| C. | 独立性检验得到的结论一定正确 | |
| D. | 利用随机变量X2来判断“两个独立事件X、Y的关系”时,算出的X2值越大,判断“X、Y有关”的把握越大 |
17.若复数z=-9-i,则$\overrightarrow{z}$在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.下列各组函数中,f(x)与g(x)相等的一组是( )
| A. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ | B. | f(x)=|x-1|,g(x)=$\left\{\begin{array}{l}{x-1(x≥1)}\\{1-x(x<1)}\end{array}\right.$ | ||
| C. | f(x)=1,g(x)=$\frac{|x|}{x}$ | D. | f(x)=$\frac{{x}^{2}-9}{x+3}$,g(x)=x-3 |