题目内容
【题目】(某保险公司有一款保险产品的历史户获益率(获益率=获益÷保费收入)的频率分布直方图如图所示: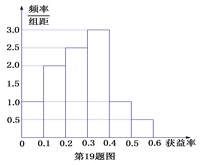
(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验若每份保单的保费在 ![]() 元的基础上每增加
元的基础上每增加 ![]() 元,对应的销量
元,对应的销量 ![]() (万份)与
(万份)与 ![]() (元)有较强线性相关关系,从历史销售记录中抽样得到如下
(元)有较强线性相关关系,从历史销售记录中抽样得到如下 ![]() 组
组 ![]() 与
与 ![]() 的对应数据:
的对应数据:
|
|
|
|
|
|
销量 |
|
|
|
|
|
(ⅰ)根据数据计算出销量 ![]() (万份)与
(万份)与 ![]() (元)的回归方程为
(元)的回归方程为 ![]() ;
;
(ⅱ)若把回归方程 ![]() 当作
当作 ![]() 与
与 ![]() 的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
的线性关系,用(Ⅰ)中求出的平均获益率估计此产品的获益率,每份保单的保费定为多少元时此产品可获得最大获益,并求出该最大获益.
参考公示: 
【答案】解:(Ⅰ)区间中值依次为:0.05,0.15,0.25,0.35,0.45,0.55,取值概率依次为:0.1,0.2,0.25,0.3,0.1,0.05,
平均获益率为 ![]()
(Ⅱ)(i)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||

则 ![]() 即
即 ![]() .
.
(ii)设每份保单的保费为 ![]() 元,则销量为
元,则销量为 ![]() ,则保费获益为
,则保费获益为![]() 万元,
万元, ![]()
当 ![]() 元时,保费收入最大为
元时,保费收入最大为 ![]() 万元,保险公司预计获益为
万元,保险公司预计获益为 ![]() 万元.
万元.
【解析】(1)由图可知求出满足条件的概率值进而求出平均获益率的值。(2)根据图表求出线性回归的样本点中心进而求出回归直线方程。(3)根据题意求出函数的解析式利用二次函数在指定区间上的最值。
【考点精析】通过灵活运用二次函数在闭区间上的最值和频率分布直方图,掌握当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() ;频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息即可以解答此题.
;频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息即可以解答此题.

练习册系列答案
相关题目




