题目内容
18.已知在△ABC中,sinA与sinB的等差中项为$\frac{7}{10}$.等比中项为$\frac{2\sqrt{3}}{5}$,则sinC+sin(A-B)=$\frac{18}{25}$或$\frac{32}{25}$..分析 由条件利用等差中项、等比中项的定义和性质求得sinA、sinB的值,可得cosA、cosB的值,再利用两角和差的正弦公式、诱导公式求得sinC+sin(A-B)的值.
解答 解:△ABC中,∵sinA与sinB的等差中项为$\frac{7}{10}$,等比中项为$\frac{2\sqrt{3}}{5}$,
∴sinA+sinB=$\frac{7}{5}$,sinA•sinB=$\frac{12}{25}$,∴sinA=$\frac{3}{5}$、sinB=$\frac{4}{5}$,或 sinA=$\frac{4}{5}$、sinB=$\frac{3}{5}$,
∴当sinA=$\frac{3}{5}$、sinB=$\frac{4}{5}$ 时,cosA=$\sqrt{{1-sin}^{2}A}$=$\frac{4}{5}$,cosB=$\sqrt{{1-sin}^{2}B}$=$\frac{3}{5}$,
sinC+sin(A-B)=sin(A+B)+sin(A-B)=2sinAcosB=2•$\frac{3}{5}$•$\frac{3}{5}$=$\frac{18}{25}$.
∴当sinA=$\frac{4}{5}$、sinB=$\frac{3}{5}$,cosA=$\sqrt{{1-sin}^{2}A}$=$\frac{3}{5}$,cosB=$\sqrt{{1-sin}^{2}B}$=$\frac{4}{5}$.
sinC+sin(A-B)=sin(A+B)+sin(A-B)=2sinAcosB=2•$\frac{4}{5}$•$\frac{4}{5}$=$\frac{32}{25}$,
故答案为:$\frac{18}{25}$或$\frac{32}{25}$.
点评 本题主要考查等差中项、等比中项的定义和性质,两角和差的正弦公式、诱导公式的应用,属于基础题.

 阅读快车系列答案
阅读快车系列答案| 广告费用x(万元) | 2 | 3 | 5 | 6 |
| 销售利润y(万元) | 5 | 7 | 9 | 11 |
| A. | $\hat b>0$ | B. | $\hat a>0$ | C. | 直线l过点(4,8) | D. | 直线l过点(2,5) |
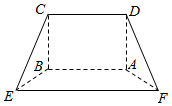 如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF.
如图,在多面体ABCDEF中,四边形ABCD是矩形,四边形ABEF为等腰梯形,且AB∥EF,AF=2,EF=2AB=4AD=4$\sqrt{2}$,平面ABCD⊥平面ABEF. 某次考试无纸化阅卷的评分规则的程序如图所示,x1,x2,x3为三个评卷人对同一道题的独立评分,p为该题的最终得分,当x1=6,x2=9,p=8.5时,x3=( )
某次考试无纸化阅卷的评分规则的程序如图所示,x1,x2,x3为三个评卷人对同一道题的独立评分,p为该题的最终得分,当x1=6,x2=9,p=8.5时,x3=( ) 如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,D为棱BB1上一点,B1D=1,E为线段AC上一点,AE=3.
如图,直三棱柱ABC-A1B1C1中,AB=AC=AA1=4,D为棱BB1上一点,B1D=1,E为线段AC上一点,AE=3.