题目内容
设直线l1的方向向量是:
=(1+cosα,sinα),α∈(0,π),直线l2的方向向量为
=(1-cosβ,sinβ),β∈(π,2π),直线l3的方向得量是
=(1,0),l1与l3的夹角为θ1,l2到l3的角为θ2,若θ1-θ2=
,试求sin(π+
)的值.
| a |
| b |
| c |
| π |
| 6 |
| α-β |
| 4 |
分析:根据直线的方向向量分别求出直线的斜率,再根据到角、夹角公式将θ1-θ2=
,转化为α,β的关系,整体代入求解.
| π |
| 6 |
解答:解:由题意得l1的斜率k1=
=
=tan
,
∵l3的方向向量是
=(1,0),
∴k3=0,
∴l1与l3的夹角为tanθ1=|tan
|,又α∈(0,π),
∴θ1=
l2的斜率k2=
=
=cot
∴l2到l3的角tanθ2=-cot
,
∵β∈(π,2π),
∴θ2=
-
∵θ1-θ2=
,
∴
-(
-
)=
,
∴
=-
,
∴sin(π+
)=-sin(
)=-sin(-
)=
| sinα |
| 1+cosα |
2sin
| ||||
1+2cos2
|
| α |
| 2 |
∵l3的方向向量是
| c |
∴k3=0,
∴l1与l3的夹角为tanθ1=|tan
| α |
| 2 |
∴θ1=
| α |
| 2 |
l2的斜率k2=
| sinβ |
| 1-cosβ |
2sin
| ||||
1-(1-2sin2
|
| β |
| 2 |
∴l2到l3的角tanθ2=-cot
| β |
| 2 |
∵β∈(π,2π),
∴θ2=
| β |
| 2 |
| π |
| 2 |
∵θ1-θ2=
| π |
| 6 |
∴
| α |
| 2 |
| β |
| 2 |
| π |
| 2 |
| π |
| 6 |
∴
| α-β |
| 2 |
| π |
| 3 |
∴sin(π+
| α-β |
| 4 |
| α-β |
| 4 |
| π |
| 6 |
| 1 |
| 2 |
点评:本题考查直线的方向向量的集合意义,直线到角、夹角公式,以及三角函数式的化简求值.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
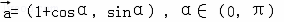 ,直线l2的方向向量为
,直线l2的方向向量为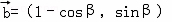 ,β∈(π,2π),直线l3的方向得量是
,β∈(π,2π),直线l3的方向得量是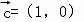 ,l1与l3的夹角为θ1,l2到l3的角为θ2,若
,l1与l3的夹角为θ1,l2到l3的角为θ2,若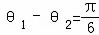 ,试求
,试求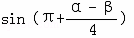 的值.
的值.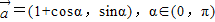 ,直线l2的方向向量为
,直线l2的方向向量为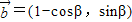 ,β∈(π,2π),直线l3的方向得量是
,β∈(π,2π),直线l3的方向得量是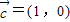 ,l1与l3的夹角为θ1,l2到l3的角为θ2,若
,l1与l3的夹角为θ1,l2到l3的角为θ2,若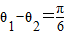 ,试求
,试求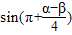 的值.
的值.